Voïvodie d'Ostrołęka





Page d'aide sur l'homonymie Pour les articles homonymes, voir Ostrołęka (homonymie).




































Voïvodie d'Ostrołęka
województwo ostrołęckie.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")}
Administration

Pays
Drapeau de la Pologne Pologne
Capitale (Diétine)
Ostrołęka
Démographie

Population
 411 600 hab. (1998)
Densité 63 hab./km2
Géographie

Superficie
649 800 ha = 6 498 km2
Localisation

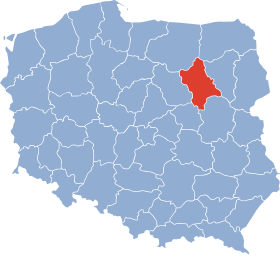Localisation de Voïvodie d'Ostrołęka
Localisation de la voïvodie de 1975 à 1998

modifier Consultez la documentation du modèle

La voïvodie d'Ostrołęka (en polonais województwo ostrołęckie) était une unité de division administrative et un gouvernement local de Pologne entre 1975 et 1998.


Elle était issue de la division de la voïvodie de Varsovie.

Elle fut remplacée en 1999 par la voïvodie de Mazovie, à la suite d'une loi de 1998 réorganisant le découpage administratif du pays.


Sa capitale était Ostrołęka.



Villes principales |




Carte de la voïvodie d'Ostrołęka


Recensement du 31.12.1998




  • POL Ostrołęka COA.svgOstrołęka - 55 271


  • POL Wyszków COA.svg Wyszków - 26 154


  • Herb ostrowi.svg Ostrów Mazowiecka - 22 592


  • POL Przasnysz COA.svg Przasnysz - 17 556


  • POL Maków Mazowiecki COA.svg Maków Mazowiecki - 10 651


  • POL Tłuszcz COA.svg Tłuszcz - 6 708


  • POL Różan COA.svg Różan - 2 906


  • POL Myszyniec COA.svg Myszyniec - 2 815


  • POL Chorzele alt COA.svg Chorzele - 2 643


  • POL gmina Brok COA.svg Brok - 1 918



District (Powiat) |


La Voïvodie d'Ostrołęka était constitué des powiaty (pluriel de Powiat) suivantes:




  • Powiat de Maków - gminy: Krasnosielc, Sypniewo, Młynarze, Płoniawy-Bramura, Czerwonka, Różan, Rzewnie, Szelków et Maków Mazowiecki.


  • Powiat d'Ostrołęka - gminy:Baranowo, Czarnia, Czerwin, Goworowo, Kadzidło, Lelis, Łyse, Myszyniec, Olszewo-Borki, Rzekuń et Troszyn.


  • Powiat d'Ostrów - gminy: Brok, Małkinia Górna, Ostrów Mazowiecka, Stary Lubotyń et Wąsewo.


  • Powiat de Przasnysz - gminy: Chorzele, Jednorożec, Krzynowłoga Mała et Przasnysz.


  • Powiat de Pułtusk - gminy: Obryte et Zatory.


  • Powiat de Szczytno - dans la Voïvodie de Varmie-Mazurie, Gmina Rozogi.


  • Powiat de Wołomin - gminy: Dąbrówka Klembów et Tłuszcz.


  • Powiat de Wyszków - gminy: Brańszczyk, Długosiodło, Rząśnik, Somianka, Wyszków et Zabrodzie.



Démographie |

















  • Portail de la Pologne Portail de la Pologne



-

Popular posts from this blog

Quarter-circle Tiles

Image
up vote 0 down vote favorite I have $99$ identical square tiles, each with a quarter-circle drawn on it like this: [asy] size(1.5cm); draw(Arc((2,0),1,90,180),red+1); draw((0,0)--(2,0)--(2,2)--(0,2)--(0,0)); [/asy] When I arrange the tiles in a $9times 11$ rectangular grid, each with a random orientation, what is the expected value of the number of full circles I form? I think this problem has to do with finding the chance any given 2x2 square has a circle, but I can't find it. expected-value share | cite | improve this question asked Nov 20 at 15:03 6minecraftninja 1 2
Read more

build a pushdown automaton that recognizes the reverse language of a given pushdown automaton?

Image
0 I think it's similiar to NFAs. I replace the finite states of the given automaton for start-states for my new automaton. I do it with $epsilon$ -transition from the start state to the actual finite states of the given automaton. The start state of the given automaton will be my accepting(finite) state of my new one. All transitions will be reversed of course to recognize the reversed word. But how do I have to change the stack of the pushdown automaton? That's tricky. formal-languages automata context-free-grammar share | cite | improve this question edited Nov 29 '18 at 14:20 joee
Read more

Mont Emei

Image
Mont Emei.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")} Vue du sommet Wanfo du mont Emei Géographie Altitude 3 099  m , Wanfo Coordonnées 29° 31′ 11″ nord, 103° 19′ 57″ est Administration Pays   Chine Province Sichuan Ville-préfecture Leshan Géolocalisation sur la carte : Sichuan Mont Emei Géolocalisation sur la carte : Chine Mont Emei modifier   Paysage panoramique du mont Emei, incluant le paysage panoramique du grand Bouddha de Leshan *   Patrimoine mondial de l'UNESCO Passerelle en bois sur le versant ouest Pays   Chine Subdivision Sichuan Type Mixte Critères (iv) (vi) (x) Superficie 15 400 ha Numéro d’identification 779 Zone géographique Asie et Pacifique  ** Année d’inscription 1996 (20 e session) * Descriptif officiel UNESCO ** Classification géog
Read more