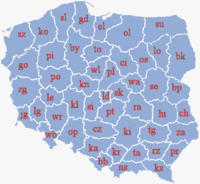
Voïvodie de Biała Podlaska

Multi tool use
Multi tool use





Page d'aide sur l'homonymie Pour les articles homonymes, voir Biała Podlaska (homonymie).







































Voïvodie de Biała Podlaska
województwo bialskopodlaskie.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")}
Blason de Voïvodie de Biała Podlaska
Administration

Pays
Drapeau de la Pologne Pologne
Capitale (Diétine)
Biała Podlaska
Démographie

Population
 661 400 hab. (1998)
Densité 124 hab./km2
Géographie

Superficie
534 800 ha = 5 348 km2
Localisation

Localisation de Voïvodie de Biała Podlaska
Localisation de la voïvodie de 1975 à 1998

modifier Consultez la documentation du modèle

La voïvodie de Biała Podlaska (en polonais : województwo bialskopodlaskie) était une unité de division administrative et un gouvernement local de Pologne entre 1975 et 1998.


Son territoire s'étendait sur 5 348 km2 et il est désormais couvert par la voïvodie de Lublin.


En 1998, la voïvodie comptait 661 400 habitants.


La capitale de la voïvodie était Biała Podlaska.


Cette voïvodie a le pourcentage le plus élevé des Biélorusses ethniques en Pologne.



Villes |


Population au 31 décembre 1998 :




  • POL Biała Podlaska COA.svgBiała Podlaska - 59 047


  • POL Międzyrzec Podlaski COA.svg Międzyrzec Podlaski - 18 274


  • POL Radzyń Podlaski COA.svg Radzyń Podlaski - 16 852


  • POL Parczew COA.svg Parczew - 11 090


  • POL Łosice COA.svg Łosice - 7205


  • Terespol herb.svg Terespol - 6002



Bureaux de district |


Sur la base de la loi du 22 mars 1990, les autorités locales de l'administration publique générale,ont créé 3 régions administratives associant une douzaine de municipalités.


Bureau de district de Biała Podlaska

  • Gminy


  1. Biała Podlaska

  2. Hanna

  3. Huszlew

  4. Janów Podlaski

  5. Kodeń

  6. Konstantynów

  7. Leśna Podlaska

  8. Łomazy

  9. Łosice

  10. Olszanka

  11. Piszczac

  12. Platerów

  13. Rokitno

  14. Rossosz

  15. Sarnaki

  16. Sławatycze

  17. Sosnówka

  18. Stara Kornica

  19. Terespol

  20. Tuczna

  21. Wisznice

  22. Zalesie


  • Villes


  1. Biała Podlaska

  2. Terespol


Bureau de district de Parczew

  • Gminy


  1. Dębowa Kłoda

  2. Jabłoń

  3. Milanów

  4. Parczew

  5. Podedwórze

  6. Siemień


Bureau de district de Radzyń Podlaski

  • Gminy


  1. Czemierniki

  2. Drelów

  3. Kąkolewnica Est

  4. Komarówka Podlaska

  5. Międzyrzec Podlaski

  6. Radzyń Podlaski

  7. Ulan-Majorat

  8. Wohyń


  • Villes


  1. Międzyrzec Podlaski

  2. Radzyń Podlaski



Démographie |



















  • Portail de la Pologne Portail de la Pologne



QpWYXpyN4M4,lbLbZdHswJiKavUMK2r5CCj7Kp20d Rpx7ZHPe2 CiExq x,6YxqWka6N1bqs6W26T,iGy5jx0
-
iTkBbGUnOdkX0T,IGhpcfmHYpA8qgkgXxR1h 1DUq u6fse,yZnevmFDaxS5gSLLspLWFU0U,1

Popular posts from this blog

Orthoptera

Image
Pour une classification, voir Orthoptera (classification phylogénétique). Orthoptera Romalea guttata , Orthoptera Caelifera Classification Règne Animalia Embranchement Arthropoda Sous-embr. Hexapoda Classe Insecta Sous-classe Dicondylia Infra-classe Pterygota Division Neoptera Super-ordre Orthopterodea Ordre Orthoptera Latreille, 1793 Les orthoptères ou Orthoptera (du grec orthos , droit, et ptéron , aile) sont un ordre de la classe des insectes. Ces animaux se caractérisent par des ailes alignées avec le corps. On estime à 22 000 le nombre d'espèces présentes sur la planète. La grande majorité est phytophage (qui se nourrit de végétaux) bien que plusieurs espèces soient régulièrement prédatrices. Cet ordre est scindé en deux sous-ordres : les ensifères (grillons et sauterelles) et les caelifères (criquets). Sommaire 1 Distribution 2 Description 2.1 Morphologie 2.2 Régime alimentai...
Read more

Ellipse (mathématiques)

Image
Pour les articles homonymes, voir Ellipse. L'ellipse est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante. Section du cône ou projection du cercle. En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre : c'est une conique d'excentricité strictement comprise entre 0 et 1. On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple). Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane. On retrouve aussi, en première approximation [ 1 ] , des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites arti...
Read more

Quarter-circle Tiles

Image
up vote 0 down vote favorite I have $99$ identical square tiles, each with a quarter-circle drawn on it like this: [asy] size(1.5cm); draw(Arc((2,0),1,90,180),red+1); draw((0,0)--(2,0)--(2,2)--(0,2)--(0,0)); [/asy] When I arrange the tiles in a $9times 11$ rectangular grid, each with a random orientation, what is the expected value of the number of full circles I form? I think this problem has to do with finding the chance any given 2x2 square has a circle, but I can't find it. expected-value share | cite | improve this question asked Nov 20 at 15:03 6minecraftninja 1 2 ...
Read more