Krdytkyu

Pour les articles homonymes, voir Aire.

Cet article est une ébauche concernant les neurosciences, la médecine et la biologie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

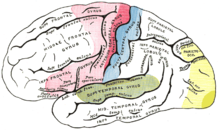
Quelques exemples d'aires fonctionnelles dans le néocortex humain

	Aire motrice primaire
	Aire motrice supplémentaire
	Aire somatosensorielle primaire
	Aire d'association sensorielle
	Aire auditive primaire
	Aire visuelle primaire

Une aire cérébrale correspond à une zone du cerveau (ou du cortex cérébral, s'agissant d'une aire corticale) selon un découpage qui peut être soit purement anatomique, soit fonctionnel. En effet, suivant les approches, ce découpage se fonde soit sur la cytoarchitectonie, c'est-à-dire sur les propriétés histologiques des neurones, soit sur le rôle de ces neurones dans la cognition, tel qu'on peut le mettre en évidence par les outils des neurosciences cognitives. On observe qu'il existe une certaine correspondance entre ces deux types de divisions. Par exemple, l'aire de Brodmann n°4, caractérisée par l'absence de couche granulaire interne, correspond très exactement au cortex moteur primaire qui dirige l'exécution des mouvements.

Les relations phylogénétiques entre les espèces font qu'il est possible de retrouver des correspondances dans l'arrangement des aires cérébrales. Par exemple, Korbinian Brodmann s'est servi de la cartographie cytoarchitectonique qu'il avait établi sur un cerveau de macaque pour définir la cartographie du cerveau humain, s'appuyant sur la très grande similarité morphologique entre les cerveaux de ces deux espèces.

Par ailleurs, bien que le cerveau conserve la même forme générale d'un individu à l'autre d'une même espèce, il existe des différences anatomiques qui font que la taille et la position exacte des aires cérébrales varient légèrement entre les individus.

• Portail des neurosciences
• Portail de la médecine