Degen





Page d'aide sur l'homonymie Pour les articles homonymes, voir Degen (homonymie).













































































Degen.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")}

Degen
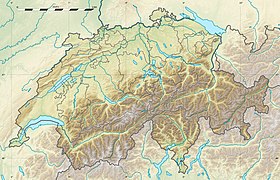
Vue du village de Degen

Blason de Degen
Héraldique
Administration

Pays
Drapeau de la Suisse Suisse

Canton
Drapeau du canton des Grisons Grisons

Région
Surselva

Commune
Lumnezia

NPA
 7145

N° OFS
 3594
Démographie

Population
permanente
 234 hab. (31 décembre 2017)
Densité 35 hab./km2
Géographie

Coordonnées
46° 42′ 00″ nord, 9° 10′ 00″ est

Altitude
 1 122 m

Superficie
 6,74 km2
Divers

Langue
Romanche
Localisation


Géolocalisation sur la carte : canton des Grisons



Voir sur la carte administrative du Canton des Grisons

City locator 14.svg

Degen





Géolocalisation sur la carte : Suisse



Voir la carte administrative de Suisse

City locator 14.svg

Degen





Géolocalisation sur la carte : Suisse



Voir la carte topographique de Suisse

City locator 14.svg

Degen





Sources
Référence population suisse[1]
Référence superficie suisse[2]


modifier Consultez la documentation du modèle

Degen (.mw-parser-output .prononciation>a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/8/8a/Loudspeaker.svg/11px-Loudspeaker.svg.png")center left no-repeat;padding-left:15px;font-size:smaller}[ˈdeɟən], allemand : Igels) est une localité et une ancienne commune suisse du canton des Grisons, située dans la région de Surselva.



Histoire |


Le 1er janvier 2013, la commune a fusionné avec Cumbel, Lumbrein, Morissen, Suraua, Vignogn, Vella et Vrin pour former la nouvelle commune Lumnezia.



Références |




  1. ↑ « Population résidente permanente et non permanente selon la région, le sexe, le lieu de naissance et l'état civil, en 2017 », sur Office fédéral de la Statistique (consulté le 30 septembre 2018).


  2. ↑ « Statistique de la superficie 2004/09 : Données communales », sur Office fédéral de la Statistique (consulté le 26 août 2017)


.mw-parser-output .autres-projets ul{margin:0;padding:0}.mw-parser-output .autres-projets li{list-style-type:none;list-style-image:none;margin:0.2em 0;text-indent:0;padding-left:24px;min-height:20px;text-align:left}.mw-parser-output .autres-projets .titre{text-align:center;margin:0.2em 0}.mw-parser-output .autres-projets li a{font-style:italic}

Sur les autres projets Wikimedia :




  • Degen, sur Wikimedia Commons




  • Portail du canton des Grisons Portail du canton des Grisons



-

Popular posts from this blog

Ellipse (mathématiques)

Image
Pour les articles homonymes, voir Ellipse. L'ellipse est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante. Section du cône ou projection du cercle. En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre : c'est une conique d'excentricité strictement comprise entre 0 et 1. On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple). Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane. On retrouve aussi, en première approximation [ 1 ] , des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites arti...
Read more

Quarter-circle Tiles

Image
up vote 0 down vote favorite I have $99$ identical square tiles, each with a quarter-circle drawn on it like this: [asy] size(1.5cm); draw(Arc((2,0),1,90,180),red+1); draw((0,0)--(2,0)--(2,2)--(0,2)--(0,0)); [/asy] When I arrange the tiles in a $9times 11$ rectangular grid, each with a random orientation, what is the expected value of the number of full circles I form? I think this problem has to do with finding the chance any given 2x2 square has a circle, but I can't find it. expected-value share | cite | improve this question asked Nov 20 at 15:03 6minecraftninja 1 2 ...
Read more

Mont Emei

Image
Mont Emei.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")} Vue du sommet Wanfo du mont Emei Géographie Altitude 3 099  m , Wanfo Coordonnées 29° 31′ 11″ nord, 103° 19′ 57″ est Administration Pays   Chine Province Sichuan Ville-préfecture Leshan Géolocalisation sur la carte : Sichuan Mont Emei Géolocalisation sur la carte : Chine Mont Emei modifier   Paysage panoramique du mont Emei, incluant le paysage panoramique du grand Bouddha de Leshan *   Patrimoine mondial de l'UNESCO Passerelle en bois sur le versant ouest Pays   Chine Subdivision Sichuan Type Mixte Critères (iv) (vi) (x) Superficie 15 400 ha Numéro d’identification 779 Zone géographique Asie et Pacifique  ** Année d’inscription 1996 (20 e session) * Descriptif officiel UNESCO ** Classification géog...
Read more