Dinitrate d'isosorbide

Multi tool use
Multi tool use





































































Dinitrate d'isosorbide


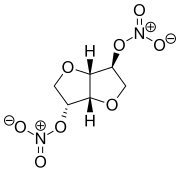
Isosorbide dinitrate structure.svg
Structure du dinitrate d'isosorbide
Identification

Nom UICPA
1,4:3,6-dianhydro-2,5-di-O-nitro-D-glucitol

No CAS
87-33-2
NoECHA
 100.001.583

No EC
 201-740-9

Code ATC
C01DA08
DrugBank
DB00883

PubChem
6883
ChEBI
6061

SMILES
[H][C@]12OC[C@H](O[N+]([O-])=O)[C@@]1([H])OC[C@H]2O[N+]([O-])=O
PubChem, vue 3D

InChI

Std. InChI : vue 3D
InChI=1S/C6H8N2O8/c9-7(10)15-3-1-13-6-4(16-8(11)12)2-14-5(3)6/h3-6H,1-2H2/t3-,4+,5-,6-/m1/s1
Std. InChIKey :
MOYKHGMNXAOIAT-JGWLITMVSA-N
Propriétés chimiques

Formule brute
C6H8N2O8  [Isomères]

Masse molaire[1]
 236,1363 ± 0,0082 g/mol
C 30,52 %, H 3,41 %, N 11,86 %, O 54,2 %,
Unités du SI et CNTP, sauf indication contraire.

modifier Consultez la documentation du modèle

Le dinitrate d'isosorbide, est un composé organique de la famille des esters de nitrate. Ce dérivé nitré est notamment utilisé comme vasodilatateur, seul ou en association, pour traiter notamment l'insuffisance cardiaque, l'angine de poitrine, l'œdème aigu du poumon, le spasme coronarien (angor de Prinzmetal) et les torsades de pointes[2]. Il peut également être utilisé en cas de fissure anale afin de faciliter la cicatrisation en assurant une irrigation sanguine suffisante.


Il agit par l'intermédiaire du monoxyde d'azote, qui induit la relaxation des muscles lisses vasculaires par l'intermédiaire du GMP cyclique.


Comme tous les dérivés nitrés, le dinitrate d'isosorbide perd progressivement en efficacité par tachyphylaxie (en). Il provoque fréquemment des céphalées par son effet vasodilatateur, ainsi que des étourdissements. Il doit être dosé précisément afin de contrôler efficacement la pression artérielle.


Il fait partie de la liste des médicaments essentiels de l'Organisation mondiale de la santé (liste mise à jour en avril 2013)[3].



Voir aussi |


  • Mononitrate d'isosorbide


Notes et références |





  1. ↑ Masse molaire calculée d’après « Atomic weights of the elements 2007 », sur www.chem.qmul.ac.uk.


  2. ↑
    isosorbide dinitrate sur le dictionnaire Vidal des spécialités pharmaceutiques.


  3. ↑ WHO Model List of Essential Medicines, 18th list, avril 2013




  • Portail de la chimie Portail de la chimie
  • Portail de la pharmacie Portail de la pharmacie



Fou4V6NZ,dDjXQPyNz4Y OzMTz,2T9
-
uL551GcjcSFuUk2 VtvGDE0jyKK g0XvxzOj63xz

Popular posts from this blog

Orthoptera

Image
Pour une classification, voir Orthoptera (classification phylogénétique). Orthoptera Romalea guttata , Orthoptera Caelifera Classification Règne Animalia Embranchement Arthropoda Sous-embr. Hexapoda Classe Insecta Sous-classe Dicondylia Infra-classe Pterygota Division Neoptera Super-ordre Orthopterodea Ordre Orthoptera Latreille, 1793 Les orthoptères ou Orthoptera (du grec orthos , droit, et ptéron , aile) sont un ordre de la classe des insectes. Ces animaux se caractérisent par des ailes alignées avec le corps. On estime à 22 000 le nombre d'espèces présentes sur la planète. La grande majorité est phytophage (qui se nourrit de végétaux) bien que plusieurs espèces soient régulièrement prédatrices. Cet ordre est scindé en deux sous-ordres : les ensifères (grillons et sauterelles) et les caelifères (criquets). Sommaire 1 Distribution 2 Description 2.1 Morphologie 2.2 Régime alimentai...
Read more

Ellipse (mathématiques)

Image
Pour les articles homonymes, voir Ellipse. L'ellipse est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante. Section du cône ou projection du cercle. En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre : c'est une conique d'excentricité strictement comprise entre 0 et 1. On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple). Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane. On retrouve aussi, en première approximation [ 1 ] , des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites arti...
Read more

Quarter-circle Tiles

Image
up vote 0 down vote favorite I have $99$ identical square tiles, each with a quarter-circle drawn on it like this: [asy] size(1.5cm); draw(Arc((2,0),1,90,180),red+1); draw((0,0)--(2,0)--(2,2)--(0,2)--(0,0)); [/asy] When I arrange the tiles in a $9times 11$ rectangular grid, each with a random orientation, what is the expected value of the number of full circles I form? I think this problem has to do with finding the chance any given 2x2 square has a circle, but I can't find it. expected-value share | cite | improve this question asked Nov 20 at 15:03 6minecraftninja 1 2 ...
Read more