Find the terminal point when the distance is not in terms of $pi$

Multi tool use
$begingroup$
From Stewart Precalculus 5th edi, P407
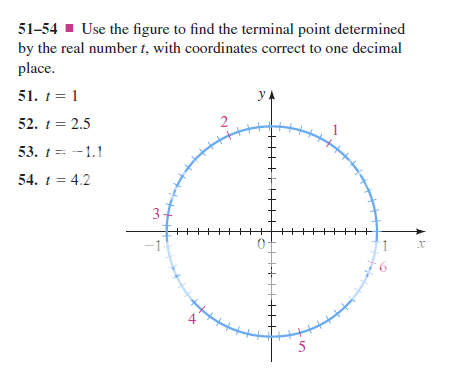
I am not sure what to do here, in the textbook, Steward didn't provide any example as to finding the terminal point when the distance $t$ is an integer. I know how to find when the distance is in terms of $pi$.
Am I supposed to replace 1 with $frac{pi}{3}$, 2 with $frac{2pi}{3}$ and give an estimation?
algebra-precalculus trigonometry
$endgroup$
add a comment |
$begingroup$
From Stewart Precalculus 5th edi, P407

I am not sure what to do here, in the textbook, Steward didn't provide any example as to finding the terminal point when the distance $t$ is an integer. I know how to find when the distance is in terms of $pi$.
Am I supposed to replace 1 with $frac{pi}{3}$, 2 with $frac{2pi}{3}$ and give an estimation?
algebra-precalculus trigonometry
$endgroup$
add a comment |
$begingroup$
From Stewart Precalculus 5th edi, P407

I am not sure what to do here, in the textbook, Steward didn't provide any example as to finding the terminal point when the distance $t$ is an integer. I know how to find when the distance is in terms of $pi$.
Am I supposed to replace 1 with $frac{pi}{3}$, 2 with $frac{2pi}{3}$ and give an estimation?
algebra-precalculus trigonometry
$endgroup$
From Stewart Precalculus 5th edi, P407

I am not sure what to do here, in the textbook, Steward didn't provide any example as to finding the terminal point when the distance $t$ is an integer. I know how to find when the distance is in terms of $pi$.
Am I supposed to replace 1 with $frac{pi}{3}$, 2 with $frac{2pi}{3}$ and give an estimation?
algebra-precalculus trigonometry
algebra-precalculus trigonometry
edited Mar 9 '17 at 17:30
Community♦
1
1
asked May 23 '13 at 10:48
BenBen
170212
170212
add a comment |
add a comment |
2 Answers
2
active
oldest
votes
$begingroup$
Looking at the figure you can see that he has labels around the edges of the circle. The numbers $1,2,3,4,5,$ and $6$. The terminal point when $t=1$ would correspond to the location labelled with a $1$. The angle at that point is exactly $1$ radian which is about $57$ degrees. By counting the number of tics to get to $1$ you can determine how many radians each tick is worth and then use that to answer questions that involve a fractional number of radians such as $t=2.5$.
$endgroup$
add a comment |
$begingroup$
I looked at it a bit and was able to figure it out. First, draw a right triangle with the hypotenuse connecting the outer diameter (point 1) of the circle and the origin. The horizontal leg is the $x$ coordinate and the vertical is the $y$ coordinate of the terminal point. We know that $1$ radian is approximately $57$ degrees, and the radius of the circle is $1$. Knowing this, we can set up the trig ratio :
$sin(x) = dfrac{text{Opposite}}{text{Hypotenuse}}$
"$sin(57) = dfrac{y}{1}$" which can be simplified to "$sin(57) = y$"
If you plug this into a calculator, it will give you the length of the vertical leg, AKA the $y$ coordinate, which is approx $0.8$. Now that you know two of the side lengths of the triangle, you can use the Pythagorean theorem to figure out the third length, which is approx $0.5$. Since the horizontal leg is $0.5$ and the vertical leg is $0.8$, your coordinates will be $(0.5,0.8)$ when $t=1$. You can use this strategy for all the other problems. Hope this helps!
$endgroup$
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "69"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f400109%2ffind-the-terminal-point-when-the-distance-is-not-in-terms-of-pi%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
2 Answers
2
active
oldest
votes
2 Answers
2
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
Looking at the figure you can see that he has labels around the edges of the circle. The numbers $1,2,3,4,5,$ and $6$. The terminal point when $t=1$ would correspond to the location labelled with a $1$. The angle at that point is exactly $1$ radian which is about $57$ degrees. By counting the number of tics to get to $1$ you can determine how many radians each tick is worth and then use that to answer questions that involve a fractional number of radians such as $t=2.5$.
$endgroup$
add a comment |
$begingroup$
Looking at the figure you can see that he has labels around the edges of the circle. The numbers $1,2,3,4,5,$ and $6$. The terminal point when $t=1$ would correspond to the location labelled with a $1$. The angle at that point is exactly $1$ radian which is about $57$ degrees. By counting the number of tics to get to $1$ you can determine how many radians each tick is worth and then use that to answer questions that involve a fractional number of radians such as $t=2.5$.
$endgroup$
add a comment |
$begingroup$
Looking at the figure you can see that he has labels around the edges of the circle. The numbers $1,2,3,4,5,$ and $6$. The terminal point when $t=1$ would correspond to the location labelled with a $1$. The angle at that point is exactly $1$ radian which is about $57$ degrees. By counting the number of tics to get to $1$ you can determine how many radians each tick is worth and then use that to answer questions that involve a fractional number of radians such as $t=2.5$.
$endgroup$
Looking at the figure you can see that he has labels around the edges of the circle. The numbers $1,2,3,4,5,$ and $6$. The terminal point when $t=1$ would correspond to the location labelled with a $1$. The angle at that point is exactly $1$ radian which is about $57$ degrees. By counting the number of tics to get to $1$ you can determine how many radians each tick is worth and then use that to answer questions that involve a fractional number of radians such as $t=2.5$.
answered Jul 2 '13 at 20:41
SpencerSpencer
8,51012056
8,51012056
add a comment |
add a comment |
$begingroup$
I looked at it a bit and was able to figure it out. First, draw a right triangle with the hypotenuse connecting the outer diameter (point 1) of the circle and the origin. The horizontal leg is the $x$ coordinate and the vertical is the $y$ coordinate of the terminal point. We know that $1$ radian is approximately $57$ degrees, and the radius of the circle is $1$. Knowing this, we can set up the trig ratio :
$sin(x) = dfrac{text{Opposite}}{text{Hypotenuse}}$
"$sin(57) = dfrac{y}{1}$" which can be simplified to "$sin(57) = y$"
If you plug this into a calculator, it will give you the length of the vertical leg, AKA the $y$ coordinate, which is approx $0.8$. Now that you know two of the side lengths of the triangle, you can use the Pythagorean theorem to figure out the third length, which is approx $0.5$. Since the horizontal leg is $0.5$ and the vertical leg is $0.8$, your coordinates will be $(0.5,0.8)$ when $t=1$. You can use this strategy for all the other problems. Hope this helps!
$endgroup$
add a comment |
$begingroup$
I looked at it a bit and was able to figure it out. First, draw a right triangle with the hypotenuse connecting the outer diameter (point 1) of the circle and the origin. The horizontal leg is the $x$ coordinate and the vertical is the $y$ coordinate of the terminal point. We know that $1$ radian is approximately $57$ degrees, and the radius of the circle is $1$. Knowing this, we can set up the trig ratio :
$sin(x) = dfrac{text{Opposite}}{text{Hypotenuse}}$
"$sin(57) = dfrac{y}{1}$" which can be simplified to "$sin(57) = y$"
If you plug this into a calculator, it will give you the length of the vertical leg, AKA the $y$ coordinate, which is approx $0.8$. Now that you know two of the side lengths of the triangle, you can use the Pythagorean theorem to figure out the third length, which is approx $0.5$. Since the horizontal leg is $0.5$ and the vertical leg is $0.8$, your coordinates will be $(0.5,0.8)$ when $t=1$. You can use this strategy for all the other problems. Hope this helps!
$endgroup$
add a comment |
$begingroup$
I looked at it a bit and was able to figure it out. First, draw a right triangle with the hypotenuse connecting the outer diameter (point 1) of the circle and the origin. The horizontal leg is the $x$ coordinate and the vertical is the $y$ coordinate of the terminal point. We know that $1$ radian is approximately $57$ degrees, and the radius of the circle is $1$. Knowing this, we can set up the trig ratio :
$sin(x) = dfrac{text{Opposite}}{text{Hypotenuse}}$
"$sin(57) = dfrac{y}{1}$" which can be simplified to "$sin(57) = y$"
If you plug this into a calculator, it will give you the length of the vertical leg, AKA the $y$ coordinate, which is approx $0.8$. Now that you know two of the side lengths of the triangle, you can use the Pythagorean theorem to figure out the third length, which is approx $0.5$. Since the horizontal leg is $0.5$ and the vertical leg is $0.8$, your coordinates will be $(0.5,0.8)$ when $t=1$. You can use this strategy for all the other problems. Hope this helps!
$endgroup$
I looked at it a bit and was able to figure it out. First, draw a right triangle with the hypotenuse connecting the outer diameter (point 1) of the circle and the origin. The horizontal leg is the $x$ coordinate and the vertical is the $y$ coordinate of the terminal point. We know that $1$ radian is approximately $57$ degrees, and the radius of the circle is $1$. Knowing this, we can set up the trig ratio :
$sin(x) = dfrac{text{Opposite}}{text{Hypotenuse}}$
"$sin(57) = dfrac{y}{1}$" which can be simplified to "$sin(57) = y$"
If you plug this into a calculator, it will give you the length of the vertical leg, AKA the $y$ coordinate, which is approx $0.8$. Now that you know two of the side lengths of the triangle, you can use the Pythagorean theorem to figure out the third length, which is approx $0.5$. Since the horizontal leg is $0.5$ and the vertical leg is $0.8$, your coordinates will be $(0.5,0.8)$ when $t=1$. You can use this strategy for all the other problems. Hope this helps!
edited Dec 12 '18 at 6:10
Yadati Kiran
1,773619
1,773619
answered Dec 12 '18 at 5:46
user625566user625566
111
111
add a comment |
add a comment |
Thanks for contributing an answer to Mathematics Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f400109%2ffind-the-terminal-point-when-the-distance-is-not-in-terms-of-pi%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
IFD prOsNq X3pKCEWUqfY8gUD,F5Ip5KT GtMwMLhLRLA5dfF qO0rkxbE,qFcYj7ltWluJRwcqlKX1F5,Eg4V7PA5Ke9HZXrg8N
