Cet article est une ébauche concernant l’anatomie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Sacrum. Vue antérieure.
Sacrum. Vue postérieure.
Le sacrum, chez les vertébrés terrestres, est un os impair, médian et symétrique, formé de la soudure des vertèbres sacrées ou sacrales (cinq vertèbres sacrées chez l'homme). Il a une forme pyramidale, dont la base crâniale est appelée le promontoire sacré ; la pointe de la pyramide s'appelant l'apex.
Le sacrum est situé entre les deux os iliaques pour former le bassin osseux.
Chez la femme, le sacrum est plus large que chez l'homme.
Sommaire
1Face antérieure
2Face postérieure
3Canal sacral
4Galerie
5Bibliographie
Face antérieure |
La face antérieure, aussi appelée face pelvienne, est concave et orientée vers le bas. Sur cette face, on note la fusion des corps vertébraux ; fusion visible au niveau des lignes transverses. Les processus costiformes sont volumineux. On remarque aussi la fusion des zygapophyses. Le ligament jaune participe également à la fusion, tout en laissant huit orifices qui sont les foramens sacrés ventraux, ou trous sacrés antérieurs.
Face postérieure |
Elle est sous-cutanée et divisée dans la longueur par la crête sacrée. Cette crête est formée par la réunion des processus épineux des vertèbres sacrées et d'une échancrure, le foramen sacré, qui aboutit en bas.
Canal sacral |
Le canal sacral est un prisme triangulaire se rétrécissant vers le bas, qui suit la courbure à concavité antéro-inférieure du sacrum. Il donne naissance latéralement à quatre foramens intervertébraux, qui bifurquent pour s’ouvrir sur les faces antérieure et postérieure par les foramens sacraux.
Galerie |
Cliquez sur une vignette pour l’agrandir.
Colonne vertébrale.
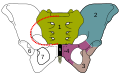
Pelvis
Vue latérale du sacrum et du coccyx.
Base du sacrum.
Coupe sagittale médiane du sacrum.
Colonne vertébrale.
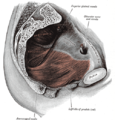
Releveur de l'anus.
branches postérieures des nerfs sacrés.
Coupe sagittale médiane du pelvis masculin.
Coupe sagittale médiane du pelvis féminin.
Bibliographie |
Raymond Richard, Lésions ostéopathiques du sacrum, Paris, Maloine SA, 1978.
Pour une classification, voir Orthoptera (classification phylogénétique). Orthoptera Romalea guttata , Orthoptera Caelifera Classification Règne Animalia Embranchement Arthropoda Sous-embr. Hexapoda Classe Insecta Sous-classe Dicondylia Infra-classe Pterygota Division Neoptera Super-ordre Orthopterodea Ordre Orthoptera Latreille, 1793 Les orthoptères ou Orthoptera (du grec orthos , droit, et ptéron , aile) sont un ordre de la classe des insectes. Ces animaux se caractérisent par des ailes alignées avec le corps. On estime à 22 000 le nombre d'espèces présentes sur la planète. La grande majorité est phytophage (qui se nourrit de végétaux) bien que plusieurs espèces soient régulièrement prédatrices. Cet ordre est scindé en deux sous-ordres : les ensifères (grillons et sauterelles) et les caelifères (criquets). Sommaire 1 Distribution 2 Description 2.1 Morphologie 2.2 Régime alimentai...
Pour les articles homonymes, voir Ellipse. L'ellipse est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante. Section du cône ou projection du cercle. En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre : c'est une conique d'excentricité strictement comprise entre 0 et 1. On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple). Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane. On retrouve aussi, en première approximation [ 1 ] , des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites arti...
up vote
0
down vote
favorite
I have $99$ identical square tiles, each with a quarter-circle drawn on it like this: [asy] size(1.5cm); draw(Arc((2,0),1,90,180),red+1); draw((0,0)--(2,0)--(2,2)--(0,2)--(0,0)); [/asy] When I arrange the tiles in a $9times 11$ rectangular grid, each with a random orientation, what is the expected value of the number of full circles I form? I think this problem has to do with finding the chance any given 2x2 square has a circle, but I can't find it.
expected-value
share | cite | improve this question
asked Nov 20 at 15:03
6minecraftninja
1 2
...
Cliquez sur une vignette pour l’agrandir.
Portail de l’anatomie 
Portail de la médecine 
