Krdytkyu

La suite de Fibonacci est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence généralement par les termes 0 et 1 (parfois 1 et 1) et ses premiers termes sont : 0, 1, 1, 2, 3, 5, 8, 13, 21, etc. (suite A000045 de l'OEIS).

Elle doit son nom à Leonardo Fibonacci qui, dans un problème récréatif posé dans l'ouvrage Liber abaci publié en 1202, décrit la croissance d'une population de lapins : « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? »

Cette suite est fortement liée au nombre d'or, φ (phi). Ce nombre intervient dans l'expression du terme général de la suite. Inversement, la suite de Fibonacci intervient dans l'écriture des réduites de l'expression de φ en fraction continue : les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or.

Croissance d'une population de lapins selon la suite de Fibonacci, jusqu'au 6^e mois.

Présentation mathématique |

Formule de récurrence |

Le problème de Fibonacci est à l'origine de la suite dont le n{displaystyle n}-ième terme correspond au nombre de paires de lapins au n{displaystyle n}-ième mois. Dans cette population (idéale), on suppose que :

• au (début du) premier mois, il y a juste une paire de lapereaux ;


• les lapereaux ne procréent qu'à partir du (début du) troisième mois ;


• chaque (début de) mois, toute paire susceptible de procréer engendre effectivement une nouvelle paire de lapereaux ;


• les lapins ne meurent jamais (donc la suite de Fibonacci est croissante).

Notons Fn{displaystyle {mathcal {F}}_{n}} le nombre de couples de lapins au début du mois n{displaystyle n}. Jusqu’à la fin du deuxième mois, la population se limite à un couple (ce qu'on note : F1=F2=1{displaystyle {mathcal {F}}_{1}={mathcal {F}}_{2}=1}).

Dès le début du troisième mois, le couple de lapins a deux mois et il engendre un autre couple de lapins ; on note alors F3=2{displaystyle {mathcal {F}}_{3}=2}.

Plaçons-nous maintenant au mois n{displaystyle n,} et cherchons à exprimer ce qu'il en sera deux mois plus tard, soit au mois n+2{displaystyle n+2} : Fn+2{displaystyle {mathcal {F}}_{n+2}} désigne la somme des couples de lapins au mois n+1{displaystyle n+1} et des couples nouvellement engendrés.

Or, n'engendrent au mois n+2{displaystyle n+2} que les couples pubères, c'est-à-dire ceux qui existent deux mois auparavant. On a donc, pour tout entier n{displaystyle n} strictement positif :

Fn+2=Fn+1+Fn{displaystyle {mathcal {F}}_{n+2}={mathcal {F}}_{n+1}+{mathcal {F}}_{n}}

On choisit alors de poser F0=0{displaystyle {mathcal {F}}_{0}=0}, de manière que cette équation soit encore vérifiée pour n = 0.

On obtient ainsi la forme récurrente de la suite de Fibonacci : chaque terme de cette suite est la somme des deux termes précédents ; pour obtenir chacun de ces deux termes, il faut faire la somme de leurs termes précédents… et ainsi de suite, jusqu'à ce que ces deux termes soient les deux termes initiaux, F1{displaystyle {mathcal {F}}_{1}} et F0{displaystyle {mathcal {F}}_{0}}, qui sont connus.

Nombres de Fibonacci |

Les termes de cette suite sont appelés nombres de Fibonacci (suite A000045 de l'OEIS) :

F0{displaystyle {mathcal {F}}_{0}}	F1{displaystyle {mathcal {F}}_{1}}	F2{displaystyle {mathcal {F}}_{2}}	F3{displaystyle {mathcal {F}}_{3}}	F4{displaystyle {mathcal {F}}_{4}}	F5{displaystyle {mathcal {F}}_{5}}	F6{displaystyle {mathcal {F}}_{6}}	F7{displaystyle {mathcal {F}}_{7}}	F8{displaystyle {mathcal {F}}_{8}}	F9{displaystyle {mathcal {F}}_{9}}	F10{displaystyle {mathcal {F}}_{10}}	F11{displaystyle {mathcal {F}}_{11}}	F12{displaystyle {mathcal {F}}_{12}}	F13{displaystyle {mathcal {F}}_{13}}	F14{displaystyle {mathcal {F}}_{14}}	F15{displaystyle {mathcal {F}}_{15}}	F16{displaystyle {mathcal {F}}_{16}}	...	Fn{displaystyle {mathcal {F}}_{n}}
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	...	Fn−1+Fn−2{displaystyle {mathcal {F}}_{n-1}+{mathcal {F}}_{n-2}}

Expression fonctionnelle |

On souhaite établir une expression fonctionnelle de la suite de Fibonacci, c'est-à-dire une expression telle que le calcul du nombre de couples pour une valeur de n donnée ne présuppose la connaissance d’aucun nombre de couples pour une quelconque autre valeur de n, ce que ne permet pas la formule de récurrence. Comme la suite de Fibonacci est linéairement récurrente d’ordre 2, son équation caractéristique est une équation du second degré :

x2−x−1=0{displaystyle x^{2}-x-1=0},

dont les deux solutions sont :

x1=φ=1+52etx2=φ′=−1φ=1−52{displaystyle x_{1}=varphi ={frac {1+{sqrt {5}}}{2}}qquad {text{et}}qquad x_{2}=varphi '=-{frac {1}{varphi }}={frac {1-{sqrt {5}}}{2}}},

où φ{displaystyle varphi } est le nombre d'or.

Les suites (φn){displaystyle (varphi ^{n})} et (φ′n){displaystyle (varphi '^{n})} engendrent alors l'espace vectoriel des suites vérifiant un+2=un+1+un{displaystyle u_{n+2}=u_{n+1}+u_{n}}. Il en résulte que :

Fn=αφn+βφ′n{displaystyle {mathcal {F}}_{n}=alpha {}varphi ^{n}+beta varphi '^{n}} (α{displaystyle alpha } et β{displaystyle beta } sont des constantes à déterminer à partir de F0{displaystyle {mathcal {F}}_{0}} et F1{displaystyle {mathcal {F}}_{1}}.)

Les conditions initiales F0=0{displaystyle {mathcal {F}}_{0}=0} et F1=1{displaystyle {mathcal {F}}_{1}=1} conduisent au système suivant :

{α+β=0α−β=25{displaystyle left{{begin{matrix}alpha +beta =0\alpha -beta ={frac {2}{sqrt {5}}}end{matrix}}right.}

ce qui donne :

α=15etβ=−15.{displaystyle alpha ={frac {1}{sqrt {5}}}qquad {text{et}}qquad beta =-{frac {1}{sqrt {5}}}.}

Nous obtenons finalement l'expression fonctionnelle recherchée, qui porte le nom de formule de Binet^[1] :

Fn=15(φn−φ′n),avecφ=1+52etφ′=−1φ.{displaystyle {mathcal {F}}_{n}={frac {1}{sqrt {5}}}(varphi ^{n}-varphi '^{n}),qquad {text{avec}}qquad varphi ={frac {1+{sqrt {5}}}{2}}qquad {text{et}}qquad varphi '=-{frac {1}{varphi }}.}

(Ces calculs restent valables pour n entier négatif quand la suite est prolongée comme ci-dessous.)

Quand n tend vers +∞, Fn{displaystyle {mathcal {F}}_{n}} est équivalent à φn5{displaystyle {frac {varphi ^{n}}{sqrt {5}}}}. Plus précisément, φn{displaystyle varphi ^{n}} tend vers l'infini et φ′n{displaystyle varphi '^{n}} tend vers zéro car |φ′|<1<φ{displaystyle |varphi '|<1<varphi }.

En fait, dès le rang n = 1, le deuxième terme φ′n5{displaystyle {varphi '^{n} over {sqrt {5}}}} est assez petit pour que les nombres de Fibonacci puissent être obtenus uniquement à partir du premier terme :

Fn{displaystyle {mathcal {F}}_{n}} est l'entier le plus proche de φn5{displaystyle {frac {varphi ^{n}}{sqrt {5}}}} (et il lui est supérieur ou inférieur, selon la parité de n).

Il existe d'autres démonstrations de la formule de Binet, telles que la transformation en Z et la technique des fonctions génératrices.

Remarquons qu'une fois découverte, cette formule se démontre aussi par récurrence (y compris pour n entier négatif).

La suite pour les nombres négatifs |

En général, on n'étudie pas les nombres de Fibonacci pour des valeurs négatives de n, bien que la formule de récurrence les définisse aussi de proche en proche :Fn=Fn+2−Fn+1{displaystyle {mathcal {F}}_{n}={mathcal {F}}_{n+2}-{mathcal {F}}_{n+1}}donc autour de 0, la suite est :

F−6{displaystyle {mathcal {F}}_{-6}}

F−5{displaystyle {mathcal {F}}_{-5}}

F−4{displaystyle {mathcal {F}}_{-4}}

F−3{displaystyle {mathcal {F}}_{-3}}

F−2{displaystyle {mathcal {F}}_{-2}}

F−1{displaystyle {mathcal {F}}_{-1}}

F0{displaystyle {mathcal {F}}_{0}}

F1{displaystyle {mathcal {F}}_{1}}

F2{displaystyle {mathcal {F}}_{2}}

F3{displaystyle {mathcal {F}}_{3}}

F4{displaystyle {mathcal {F}}_{4}}

F5{displaystyle {mathcal {F}}_{5}}

F6{displaystyle {mathcal {F}}_{6}}

−8

5

−3

2

−1

1

0

1

1

2

3

5

8

On remarque, sur ces premières valeurs, que

• si n est pair alors F−n=−Fn{displaystyle {mathcal {F}}_{-n}=-{mathcal {F}}_{n}}
  


• si n est impair alors F−n=Fn{displaystyle {mathcal {F}}_{-n}={mathcal {F}}_{n}}
  

ou plus synthétiquement :

F−n=(−1)n+1Fn.{displaystyle {mathcal {F}}_{-n}=(-1)^{n+1}{mathcal {F}}_{n}.}

On peut le démontrer pour tout entier n, par la formule de Binet ci-dessus, ou directement par récurrence.

Limite des quotients |

Comme l'avait déjà remarqué Johannes Kepler^[2], le taux de croissance des nombres de Fibonacci, c'est-à-dire Fn+1Fn{displaystyle {frac {{mathcal {F}}_{n+1}}{{mathcal {F}}_{n}}}}, converge vers le nombre d'or, φ{displaystyle varphi }.

En effet, puisque la suite Fn{displaystyle {mathcal {F}}_{n}} est équivalente à φn5{displaystyle {frac {varphi ^{n}}{sqrt {5}}}} (cf. supra, section Expression fonctionnelle), la suite
Fn+1Fn{displaystyle {frac {{mathcal {F}}_{n+1}}{{mathcal {F}}_{n}}}} est équivalente à φn+15φn5=φ,{displaystyle {frac {frac {varphi ^{n+1}}{sqrt {5}}}{frac {varphi ^{n}}{sqrt {5}}}}=varphi ,} qui est donc sa limite.

En fait plus généralement, toutes les suites vérifiant la même relation de récurrence que la suite de Fibonacci (cf. infra, section Suites de Fibonacci généralisées) satisfont cette propriété, sauf celles commençant par a et aφ'.

Bases et espaces vectoriels |

• La dénomination de « suite de Fibonacci généralisée » est attribuée plus généralement à toute fonction G{displaystyle {mathcal {G}}} définie sur ℕ vérifiant pour tout entier naturel n, Gn+2=Gn+1+Gn{displaystyle {mathcal {G}}_{n+2}={mathcal {G}}_{n+1}+{mathcal {G}}_{n}}. Ces fonctions sont précisément celles pour lesquelles il existe des nombres a et b tels que pour tout entier naturel n, Gn=aFn+bFn+1{displaystyle {mathcal {G}}_{n}=a{mathcal {F}}_{n}+b{mathcal {F}}_{n+1}}. Ainsi, l'ensemble des suites de Fibonacci est un espace vectoriel, et les suites (Fn){displaystyle ({mathcal {F}}_{n})} et (Fn+1){displaystyle ({mathcal {F}}_{n+1})} en forment une base.


• Le nombre d'or est la racine positive du polynôme x2−x−1{displaystyle x^{2}-x-1}, ainsi φ2=φ+1{displaystyle varphi ^{2}=varphi +1}. Si l'on multiplie les deux côtés par φn{displaystyle varphi ^{n}}, on obtient φn+2=φn+1+φn{displaystyle varphi ^{n+2}=varphi ^{n+1}+varphi ^{n}}, donc la fonction n↦φn{displaystyle nmapsto varphi ^{n}} est une suite de Fibonacci. La racine négative du polynôme, φ′=1−φ{displaystyle varphi '=1-varphi }, possède les mêmes propriétés, et les deux fonctions linéairement indépendantes n↦φn{displaystyle nmapsto varphi ^{n}} et n↦(1−φ)n{displaystyle nmapsto left(1-varphi right)^{n}}, forment une autre base de l'espace vectoriel.

Algorithmes de calcul des nombres de Fibonacci |

Avec la formule de Binet |

Calculer les nombres de Fibonacci à partir du nombre d'or est une possibilité très pratique. Néanmoins, la précision de calcul de la racine carrée génère des erreurs d'arrondis pour des valeurs assez grandes dépendant du système utilisé. En général, on obtient les bonnes valeurs jusqu’à F71{displaystyle {mathcal {F}}_{71}} = 308 061 521 170 129, sur ordinateur ou sur calculatrice.

Notons qu’au-delà de F79{displaystyle {mathcal {F}}_{79}}, les calculs dépassent les possibilités de calcul en notation entière, et sont alors représentés en notation scientifique. Les premiers chiffres significatifs sont alors de nouveau bien représentés par cette formule.

Détail d’un exemple d'application faisable à partir d'une calculatrice : calcul de F50{displaystyle {mathcal {F}}_{50}}.

Le nombre d’or vaut φ=1+52 ≈{displaystyle varphi ={frac {1+{sqrt {5}}}{2}} approx }1,61803398874989…, et d'après la formule de Binet, F50{displaystyle {mathcal {F}}_{50}} est l'entier le plus proche du réel φ505{displaystyle {frac {varphi ^{50}}{sqrt {5}}}}, qui le dépasse à peine. Compte tenu de l'ordre de grandeur de ce réel, le théorème des accroissements finis permet de s'assurer que pour le calculer à 0,5 près par défaut, 1,61803398874989 est une approximation suffisante de φ{displaystyle varphi }.

On trouve que le réel (1,61803398874989)⁵⁰/√5 est à peine inférieur à l'entier 12 586 269 025, d'où

F50≈φn5≈12586269025 ,{displaystyle {mathcal {F}}_{50}approx {frac {varphi ^{n}}{sqrt {5}}}approx 12586269025~,}

si bien que

F50=12586269025 .{displaystyle {mathcal {F}}_{50}=12586269025~.}

Algorithme récursif naïf |

La mise en œuvre récursive naïve qui suit la définition de la suite de Fibonacci est immédiate en appliquant la fonction donnée par l'algorithme suivant :

fonction fibo(n): 

// entrée : un nombre entier n

// sortie : le terme de rang n de la suite de Fibonacci

//

// deux premiers cas : fibo(0) est égal à 0 et fibo(1) est égal à 1

si (n ≤ 1)

  renvoyer n 

// récurrence à partir du terme de rang 2  

sinon 

  renvoyer fibo(n - 1) + fibo(n - 2)

fin de la fonction

Ce n'est cependant pas une façon judicieuse de calculer la suite de Fibonacci, car on calcule de nombreuses fois les mêmes valeurs. Le temps de calcul s'avère exponentiel (à moins d'employer une technique de mémoïsation).

Algorithme linéaire |

Un moyen bien plus efficace de calculer la suite de Fibonacci consiste à calculer simultanément deux valeurs consécutives de la suite,

c'est-à-dire en commençant avec les deux premières valeurs 0 et 1, et en remplaçant répétitivement le premier nombre par le second, et le second nombre par la somme des deux.

public static long fibonacci(int n) {

    long i = 0;

    long j = 1;

    long temp;

    for (int k = 0; k < n; k++) {

        temp = i + j;

        i = j;

        j = temp;

    }

    return i;

}

De manière équivalente à l'algorithme linéaire, on peut écrire une fonction récursive terminale. Le temps de calcul est à chaque fois proportionnel à n mais l'espace mémoire occupé n'est pas constant dans le second cas pour les langages n’optimisant pas la récursion terminale (comme Python ou Java).

Algorithme récursif terminal |

  public static long fibonacci(int n, long a, long b) {

      return (n > 0) ? fibonacci(n - 1, b, a + b) : a;       

  }

L'appel

  fibonacci(n, 0, 1)

lance le calcul pour la valeur de n donnée. En utilisant la méthode usuelle d'élimination de la récursivité terminale, on retrouve l'algorithme itératif précédent.

Algorithme corécursif |

En Haskell, on peut définir directement la suite de Fibonacci comme un stream

fibs = 0:1:zipWith (+) fibs (tail fibs) 

dont le calcul des valeurs

fibs !! n

est linéaire.

Algorithme logarithmique |

En utilisant la relation matricielle suivante, que l'on montre par récurrence :

(1110)n=(Fn+1FnFnFn−1){displaystyle {begin{pmatrix}1&1\1&0end{pmatrix}}^{n}={begin{pmatrix}{mathcal {F}}_{n+1}&{mathcal {F}}_{n}\{mathcal {F}}_{n}&{mathcal {F}}_{n-1}end{pmatrix}}}

ou avec les propriétés de la suite de Fibonacci, on obtient :

F2k=2Fk−1Fk+Fk2=(2Fk−1+Fk)Fk{displaystyle {mathcal {F}}_{2k}=2{mathcal {F}}_{k-1}{mathcal {F}}_{k}+{mathcal {F}}_{k}^{2}=(2{mathcal {F}}_{k-1}+{mathcal {F}}_{k}){mathcal {F}}_{k}}

F2k+1=Fk+12+Fk2{displaystyle {mathcal {F}}_{2k+1}={mathcal {F}}_{k+1}^{2}+{mathcal {F}}_{k}^{2}}

En prenant bien soin de ne pas calculer deux fois les mêmes éléments, on obtient alors un algorithme dont le temps de calcul^[3] est proportionnel au logarithme de n.

En retravaillant les relations de récurrence pour le cas pair on obtient :

F2k=F2k+1−F2k−1=(Fk+12+Fk2)−(Fk2+Fk−12)=Fk+12−Fk−12{displaystyle {mathcal {F}}_{2k}={mathcal {F}}_{2k+1}-{mathcal {F}}_{2k-1}=({mathcal {F}}_{k+1}^{2}+{mathcal {F}}_{k}^{2})-({mathcal {F}}_{k}^{2}+{mathcal {F}}_{k-1}^{2})={mathcal {F}}_{k+1}^{2}-{mathcal {F}}_{k-1}^{2}}

Et donc :

∀n∈Z, Fn=F⌊n2⌋+12−(−1)nF⌊n−12⌋2.{displaystyle forall nin mathbb {Z} ,~{mathcal {F}}_{n}={mathcal {F}}_{lfloor {frac {n}{2}}rfloor +1}^{2}-(-1)^{n}{mathcal {F}}_{lfloor {frac {n-1}{2}}rfloor }^{2}.}

Curiosité algorithmique |

Le programme FRACTRAN défini par la liste de fractions [23/95, 57/23, 17/39, 130/17, 11/14, 35/11, 19/13, 1/19, 35/2, 13/7, 7] et appliqué à l'entier 3 génère une suite qui contient tous les termes de la forme 2a3b{displaystyle 2^{a}3^{b}}, où a{displaystyle a} et b{displaystyle b} sont deux termes consécutifs de la suite de Fibonacci.

Série génératrice |

La série génératrice de la suite de Fibonacci^[4] donne une série entière dont le rayon de convergence vaut 1/φ (d'après le théorème de Cauchy-Hadamard ou plus simplement, la règle de d'Alembert). Pour tout complexe z de module strictement inférieur à 1/φ, la série correspondante (absolument convergente) est égale à
∑n∈NFnzn=z1−z−z2{displaystyle sum _{nin mathbb {N} }{mathcal {F}}_{n}z^{n}={frac {z}{1-z-z^{2}}}}
(donc à z∑m∈N(z+z2)m=∑m,k∈N(mk)z1+m+k{displaystyle zsum _{min mathbb {N} }(z+z^{2})^{m}=sum _{m,kin mathbb {N} }{m choose k}z^{1+m+k}}, où les coefficients binomiaux (mk){displaystyle m choose k} sont nuls pour k>m{displaystyle k>m}).

En particulier, pour tout réel k > φ,
1k2−k−1=∑n=1∞Fn×k−(n+1).{displaystyle {frac {1}{k^{2}-k-1}}=sum _{n=1}^{infty }{mathcal {F}}_{n}times k^{-(n+1)}.}

Propriétés de la suite de Fibonacci |

La suite de Fibonacci présente de remarquables propriétés. En voici quelques-unes, démontrées le plus souvent à partir de la formule de Binet ou par récurrence (pour certaines, on peut aussi utiliser le calcul matriciel et les identités données au paragraphe « algorithme logarithmique »). Nous donnons également quelques propriétés liant la suite de Fibonacci et la suite des nombres de Lucas Ln{displaystyle {mathcal {L}}_{n}} définie par la même relation de récurrence mais avec pour initialisation L0=2{displaystyle {mathcal {L}}_{0}=2} et L1=1{displaystyle {mathcal {L}}_{1}=1}, et pour laquelle l'analogue de la formule de Binet est : Ln=φn+φ′n{displaystyle {mathcal {L}}_{n}=varphi ^{n}+varphi '^{n}}.

Par une récurrence immédiate^[5] sur n∈N{displaystyle nin mathbb {N} }, Fn+1{displaystyle {mathcal {F}}_{n+1}} est égal au nombre de suites finies d'entiers égaux à 1 ou 2 dont la somme est égale à n{displaystyle n}. (On peut donc l'interpréter comme le nombre de façons différentes de paver un rectangle 2×N au moyen de dominos 2×1.)

Propriété 1 : ∀(p,q,r)∈Z3,FpFq+r−(−1)rFp−rFq=Fp+qFr,{displaystyle forall (p,q,r)in mathbb {Z} ^{3},{mathcal {F}}_{p}{mathcal {F}}_{q+r}-(-1)^{r}{mathcal {F}}_{p-r}{mathcal {F}}_{q}={mathcal {F}}_{p+q}{mathcal {F}}_{r},} ou encore : FpFq+r−FrFp+q=(−1)rFp−rFq.{displaystyle {mathcal {F}}_{p}{mathcal {F}}_{q+r}-{mathcal {F}}_{r}{mathcal {F}}_{p+q}=(-1)^{r}{mathcal {F}}_{p-r}{mathcal {F}}_{q}.}

C'est un cas particulier des identités remarquables vérifiées par les suites récurrentes linéaires d'ordre 2.

Propriété 2 : ∀(p,q)∈Z2,FpFq+1+Fp−1Fq=Fp+q.{displaystyle forall (p,q)in mathbb {Z} ^{2},{mathcal {F}}_{p}{mathcal {F}}_{q+1}+{mathcal {F}}_{p-1}{mathcal {F}}_{q}={mathcal {F}}_{p+q}.}

C'est le cas r=1{displaystyle r=1} de la propriété 1^[6].

Propriété 3 : ∀p∈Z,F2p−1=Fp−12+Fp2.{displaystyle forall pin mathbb {Z} ,{mathcal {F}}_{2p-1}={mathcal {F}}_{p-1}^{2}+{mathcal {F}}_{p}^{2}.}

C'est le cas q=p−1{displaystyle q=p-1} de la propriété 2.

Propriété 4 : ∀(p,r)∈Z2,FpFr+1−FrFp+1=(−1)rFp−r.{displaystyle forall (p,r)in mathbb {Z} ^{2},{mathcal {F}}_{p}{mathcal {F}}_{r+1}-{mathcal {F}}_{r}{mathcal {F}}_{p+1}=(-1)^{r}{mathcal {F}}_{p-r}.}

C'est le cas q=1{displaystyle q=1} de la propriété 1.

Propriété 5 : ∀(p,q)∈Z2,Fp2−Fp−qFp+q=(−1)p−qFq2{displaystyle forall (p,q)in mathbb {Z} ^{2},{mathcal {F}}_{p}^{2}-{mathcal {F}}_{p-q}{mathcal {F}}_{p+q}=(-1)^{p-q}{mathcal {F}}_{q}^{2}} (identité de Catalan) et Fp+1Fp−1−Fp2=(−1)p{displaystyle {mathcal {F}}_{p+1}{mathcal {F}}_{p-1}-{mathcal {F}}_{p}^{2}=(-1)^{p}} (identité de Cassini^[5],[7]).

L'identité de Catalan est le cas r=p−q{displaystyle r=p-q} de la propriété 1. L'identité de Cassini est le cas q=1{displaystyle q=1} de celle de Catalan (c'est donc aussi le cas r=p−1{displaystyle r=p-1} de la propriété 4).

Corollaire 1 : ∀p∈Z,Fp=Fp−1+5Fp−12−4(−1)p2 et 5Fp2+4(−1)p∈N.{displaystyle forall pin mathbb {Z} ,{mathcal {F}}_{p}={frac {{mathcal {F}}_{p-1}+{sqrt {5{mathcal {F}}_{p-1}^{2}-4(-1)^{p}}}}{2}}~{text{et}}~{sqrt {5{mathcal {F}}_{p}^{2}+4(-1)^{p}}}in mathbb {N} .}

Corollaire 2 : ∀p∈Z,Fp+2Fp+1Fp−1Fp−2−Fp4+1=0.{displaystyle forall pin mathbb {Z} ,{mathcal {F}}_{p+2}{mathcal {F}}_{p+1}{mathcal {F}}_{p-1}{mathcal {F}}_{p-2}-{mathcal {F}}_{p}^{4}+1=0.}

Propriété 6 : La suite de Fibonacci est à divisibilité (en) faible : ∀(k,n)∈Z2Fn∣Fnk{displaystyle forall (k,n)in mathbb {Z} ^{2}quad {mathcal {F}}_{n}mid {mathcal {F}}_{nk}}^[8].

Cela résulte immédiatement de la propriété 2 ou 4 (par récurrence sur |k|), ou d'un calcul explicite du quotient (en particulier, F2n=FnLn{displaystyle {mathcal {F}}_{2n}={mathcal {F}}_{n}{mathcal {L}}_{n}}). Plus généralement (par l'une ou l'autre méthode) toute suite de Lucas U(P, Q) est à divisibilité faible. La propriété 6 est aussi — lorsqu'on ne l'y utilise pas comme lemme — un corollaire de la propriété 8 ci-dessous.

Propriété 7 : Pour tout entier naturel n différent de 4, si Fn{displaystyle {mathcal {F}}_{n}} est premier, alors n est premier.

Ou par contraposée : si n{displaystyle n} est composé alors Fn{displaystyle {mathcal {F}}_{n}} aussi. En effet, supposons n=mk{displaystyle n=mk} avec m{displaystyle m} et k{displaystyle k} entiers strictement supérieurs à 1. Comme n{displaystyle n} est supposé différent de 4, l'un au moins des deux facteurs est strictement supérieur à 2 : par exemple m>2{displaystyle m>2}. D'après la propriété 6, Fm{displaystyle {mathcal {F}}_{m}} est alors un diviseur propre de Fn{displaystyle {mathcal {F}}_{n}}, qui n'est donc pas premier.

La réciproque est fausse, car 2 est premier alors que F2{displaystyle {mathcal {F}}_{2}} ne l'est pas ; de façon moins triviale, F19=4181=37×113{displaystyle {mathcal {F}}_{19}=4181=37times 113}.

Propriété 8 : La suite de Fibonacci est à divisibilité forte : ∀(a,b)∈Z×Z∗, Fa∧Fb=Fa∧b,{displaystyle forall (a,b)in mathbb {Z} times mathbb {Z} ^{*},~{mathcal {F}}_{a}land {mathcal {F}}_{b}={mathcal {F}}_{aland b},} où ∧ désigne le PGCD de nombres entiers.

En particulier, ∀n∈Z,Fn∧Fn+1=1{displaystyle forall nin mathbb {Z} ,{mathcal {F}}_{n}land {mathcal {F}}_{n+1}=1} c.-à-d. que Fn{displaystyle {mathcal {F}}_{n}} et Fn+1{displaystyle {mathcal {F}}_{n+1}} sont premiers entre eux.

Sans utiliser que l'anneau ℤ est de Bézout (ni la propriété 6), on démontre plus généralement que dans tout anneau intègre à PGCD, une suite de Lucas U(P, Q) est à divisibilité forte si (et seulement si) ses paramètres P et Q sont premiers entre eux.

Propriété 9 : ∀(p,r)∈Z2,Fp+r−(−1)rFp−r=FrLp.{displaystyle forall (p,r)in mathbb {Z} ^{2},{mathcal {F}}_{p+r}-(-1)^{r}{mathcal {F}}_{p-r}={mathcal {F}}_{r}{mathcal {L}}_{p}.} En particulier :

Fp+1+Fp−1=Lp,Fp+2−Fp−2=Lp,Fp+3+Fp−3=2Lp.{displaystyle {mathcal {F}}_{p+1}+{mathcal {F}}_{p-1}={mathcal {L}}_{p},quad {mathcal {F}}_{p+2}-{mathcal {F}}_{p-2}={mathcal {L}}_{p},quad {mathcal {F}}_{p+3}+{mathcal {F}}_{p-3}=2{mathcal {L}}_{p}.}

L'égalité est immédiate si p=0{displaystyle p=0}. Pour p≠0{displaystyle pneq 0}, c'est le cas particulier q=p{displaystyle q=p} de la propriété 1.

Propriété 10 : ∀n∈Z,φn=Fnφ+Fn−1 et φ′n=Fnφ′+Fn−1.{displaystyle forall nin mathbb {Z} ,varphi ^{n}={mathcal {F}}_{n}varphi +{mathcal {F}}_{n-1}~{text{et}}~varphi '^{n}={mathcal {F}}_{n}varphi '+{mathcal {F}}_{n-1}.}

Propriété 11 : ∀n∈N∑0≤i<nF2i+1=F2n,1+∑0≤i<nF2i=F2n−1et1+∑0≤i<nFi=Fn+1{displaystyle forall nin mathbb {N} quad sum _{0leq i<n}{mathcal {F}}_{2i+1}={mathcal {F}}_{2n},quad 1+sum _{0leq i<n}{mathcal {F}}_{2i}={mathcal {F}}_{2n-1}quad {text{et}}quad 1+sum _{0leq i<n}{mathcal {F}}_{i}={mathcal {F}}_{n+1}}^[9].

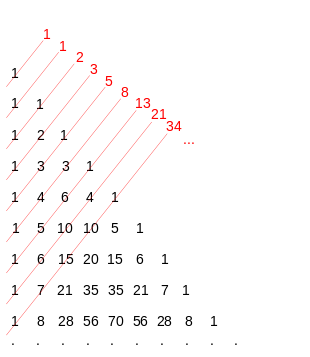
La somme des diagonales ascendantes du triangle de Pascal forme la suite de Fibonacci.

Propriété 12 : ∀n∈N, Fn=∑k∈Z(n−1−kk){displaystyle forall nin mathbb {N} ,~{mathcal {F}}_{n}=sum _{kin mathbb {Z} }{n-1-k choose k}} (somme finie car les coefficients binomiaux (n−1−kk){displaystyle {n-1-k choose k}} sont nuls si k<0{displaystyle k<0} ou si k>n−1−k{displaystyle k>n-1-k}).

Cette propriété se déduit immédiatement de l'expression de la série génératrice (voir supra). On peut aussi la démontrer par une récurrence d'ordre 2 sur n :

Cela signifie que, dans un triangle de Pascal, les nombres de Fibonacci s'obtiennent en sommant les termes situés sur une diagonale (du bas vers la droite). Les termes de ces diagonales sont d'ailleurs les coefficients des polynômes de Fibonacci ; ainsi, F6(x)=x5+4x3+3x{displaystyle F_{6}(x)=x^{5}+4x^{3}+3x} et F9(x)=x8+7x6+15x4+10x2+1{displaystyle F_{9}(x)=x^{8}+7x^{6}+15x^{4}+10x^{2}+1}.

Propriété 13 : ∀n∈N, 2n−1Fn=∑0≤k≤n/2(n2k+1)5k{displaystyle forall nin mathbb {N} ,~2^{n-1}{mathcal {F}}_{n}=sum _{0leq kleq n/2}{n choose 2k+1}5^{k}}.

Cette propriété découle du développement binomial de la formule de Binet^[10] ; on a d'ailleurs une formule analogue pour les nombres de Lucas : ∀n∈N, 2n−1Ln=∑0≤k≤n/2(n2k)5k{displaystyle forall nin mathbb {N} ,~2^{n-1}{mathcal {L}}_{n}=sum _{0leq kleq n/2}{n choose 2k}5^{k}}.

Propriété 14 : La suite (un)n∈N∗{displaystyle (u_{n})_{nin mathbb {N} ^{*}}} définie par un=Fn+1/Fn{displaystyle u_{n}={mathcal {F}}_{n+1}/{mathcal {F}}_{n}} vérifieun+1=1+1/un et un2−un−1=(−1)n/Fn2{displaystyle u_{n+1}=1+1/u_{n}{text{ et }}u_{n}^{2}-u_{n}-1=(-1)^{n}/{mathcal {F}}_{n}^{2}}^{[réf. souhaitée]}(d'après la relation de récurrence sur les Fn{displaystyle {mathcal {F}}_{n}} et l'identité de Cassini vue en propriété 5).

Propriété 15 : La factorisation des polynômes de Fibonacci permet d'exprimer les Fn{displaystyle {mathcal {F}}_{n}} (pour n ≥ 1) sous forme de produits trigonométriques^[11] :Fn=∏1≤k≤(n−1)/23+2cos⁡(2kπn){displaystyle {mathcal {F}}_{n}=prod _{1leq kleq (n-1)/2}3+2cos left({frac {2kpi }{n}}right)}.

Divisibilité des nombres de Fibonacci |

Une première approche de la question de la divisibilité de Fn{displaystyle {mathcal {F}}_{n}} par un entier a consiste à étudier la suite des restes de Fn{displaystyle {mathcal {F}}_{n}} modulo a : cette suite (r_n) vérifie (dans Z/aZ) la même récurrence (r_n+2 = r_n+1 + r_n) et est donc périodique de période au plus a² (les longueurs des périodes en fonction de a forment la suite des périodes de Pisano, suite A001175 de l'OEIS) ; on en déduit que pour tout a, il existe n inférieur ou égal à a² tel que Fn{displaystyle {mathcal {F}}_{n}} (et donc Fkn{displaystyle {mathcal {F}}_{kn}}) soit divisible par a. Plus précisément, l'étude de cette récurrence dans le corps Z/pZ (où p est un nombre premier) amène à des formules analogues à la formule de Binet, d'où l'on déduit finalement (selon que 5 est ou n'est pas un carré modulo p ; voir la loi de réciprocité quadratique) que F5n{displaystyle {mathcal {F}}_{5n}} est divisible par 5, et que si p est premier autre que 5, F(p−1)n{displaystyle {mathcal {F}}_{(p-1)n}} est divisible par p si p est de la forme 5m + 1 ou 5m + 4, et F(p+1)n{displaystyle {mathcal {F}}_{(p+1)n}} est divisible par p sinon. Des résultats plus précis peuvent d'ailleurs être obtenus ; ainsi, dans le premier cas, F(p−1)/2{displaystyle {mathcal {F}}_{(p-1)/2}} est divisible par p si (p – 1)/2 est pair^[12]. Enfin, si p > 2 est premier et divise Fn{displaystyle {mathcal {F}}_{n}}, p^k divise Fpk−1n{displaystyle {mathcal {F}}_{p^{k-1}n}}, et 2^k+1 divise F3.2k−1{displaystyle {mathcal {F}}_{3.2^{k-1}}} ; ces derniers résultats sont des conséquences du lemme de Hensel^[13],[14] ; les mêmes méthodes permettent d'obtenir des résultats analogues pour les nombres de Lucas^[12],[15].

Primalité des nombres de Fibonacci |

On découvre au fil des ans des nombres de Fibonacci premiers de plus en plus grands, mais on ignore toujours s'il en existe une infinité.

Décomposition d'un entier en somme de nombres de Fibonacci |

Tout entier positif se décompose de manière unique en la somme de nombres de Fibonacci d'indice supérieur ou égal à 2, les indices successifs de ces nombres ayant une différence supérieure ou égale à 2 lorsqu'ils sont rangés dans l'ordre.

Exemple

25=21+3+1=F8+F4+F2{displaystyle 25=21+3+1=F_{8}+F_{4}+F_{2}}.

Applications |

• En poésie, un fib est un petit poème, sorte de haïku, dont le nombre de pieds des premiers vers correspond aux premiers nombres de la suite (1, 1, 2, 3, 5, 8).


• La suite de Fibonacci apparaît dans de nombreux problèmes de dénombrement. Par exemple, le terme d'indice n (pour n supérieur ou égal à 2) de la suite de Fibonacci permet de dénombrer le nombre de façons de parcourir un chemin de longueur n-1 en faisant des pas de 1 ou 2. Ce problème apparaît d'ailleurs très tôt en Inde, sous le nom maatraameru (montagne de cadence), dans le travail du grammairien de sanskrit Pingala, le Chhandah-shastra, (l'art de la Prosodie), 450 ou 200 av. J.-C.). Le mathématicien indien Virahanka (en) en a donné des règles explicites au VIII^e siècle. Le philosophe indien Acharya Hemachandra (c. 1150) (et aussi Gopala, c. 1135) ont revisité le problème de manière assez détaillée. En sanskrit en effet, les voyelles peuvent être longues (L) ou courtes (C), et Hemachandra a souhaité calculer combien on peut former de cadences différentes d'une longueur donnée, chaque cadence étant définie par les longueurs des voyelles qui la constituent. Si la voyelle longue est deux fois plus longue que la courte, les solutions sont, en fonction de la longueur totale de la cadence :

1 C → 1

2 CC,L → 2

3 CCC, CL, LC → 3

4 CCCC, CCL, CLC, LCC, LL → 5

5 CCCCC, CCCL, CCLC, CLCC, LCCC, CLL, LCL, LLC → 8

Le nombre de cadences fait apparaître les termes de la suite de Fibonacci. En effet, une cadence de longueur n peut être constituée en ajoutant C à une cadence de longueur n – 1, ou L à une cadence de longueur n – 2. Ainsi, le nombre de cadences de longueur n est la somme des deux nombres précédents de la suite. Ce problème est également équivalent au problème de bin packing pour n articles de longueur 1 ou 2, tel qu'on le trouve par exemple dans The Art of Computer Programming de Donald Knuth.

• Les nombres de Fibonacci interviennent dans l'étude de l'exécution de l'algorithme d'Euclide qui détermine le plus grand commun diviseur de deux entiers.


• Ils sont l'outil (grâce à la propriété 8 et la factorisation de F19{displaystyle {mathcal {F}}_{19}}) d'une démonstration originale du théorème d'Euclide sur les nombres premiers^[16].


• 
  Matiyasevich a montré que les nombres de Fibonacci pouvaient être définis par une équation diophantienne, ce qui a conduit à la résolution du dixième problème de Hilbert. En 1975, Jones en a déduit que, pour des valeurs de x et y entières positives ou nulles, les valeurs positives du polynôme 2xy4+x2y3−2x3y2−y5−x4y+2y{displaystyle 2xy^{4}+x^{2}y^{3}-2x^{3}y^{2}-y^{5}-x^{4}y+2y} étaient exactement les nombres de Fibonacci. Ces valeurs positives s'obtiennent d'ailleurs en attribuant pour valeurs à x et y deux nombres de Fibonacci successifs.


• Les nombres de Fibonacci apparaissent dans la formule des diagonales du triangle de Pascal (voir Propriétés, Propriété 12).

Les carrés de Fibonacci en spirale s'ajustent ensemble pour former une spirale d'or.

• Une bonne approximation d'un rectangle d'or peut être construite à l'aide de carrés dont les côtés sont égaux aux nombres de Fibonacci.

Approximation d'une spirale d'or créée en dessinant des arcs de cercle reliant les coins opposés de carrés dans un pavage Fibonacci. Celui-ci utilise des carrés de tailles 1, 1, 2, 3, 5, 8, 13, 21, et 34.

• Une spirale logarithmique peut être approchée de la manière suivante : on commence à l'origine d'un repère cartésien, on se déplace de F1{displaystyle {mathcal {F}}_{1}} unités vers la droite, puis de F2{displaystyle {mathcal {F}}_{2}} unités vers le haut, on se déplace de F3{displaystyle {mathcal {F}}_{3}} unités vers la gauche, ensuite de F4{displaystyle {mathcal {F}}_{4}} unités vers le bas, puis de F5{displaystyle {mathcal {F}}_{5}} unités vers la droite, etc. Cela ressemble à la construction mentionnée dans l'article sur le nombre d'or.


• Les nombres de Fibonacci apparaissent souvent dans la nature lorsque des spirales logarithmiques sont construites à partir d'une unité discrète, telles que dans les tournesols ou dans les pommes de pin. Le nombre de pétales de la marguerite (et d'autres fleurs composées comme le tournesol) appartient à la suite de Fibonacci : souvent 34, 55 ou 89. Cela s'explique par le mécanisme de développement de la plante (voir le paragraphe « Phyllotaxie » de l'article sur le nombre d'or).


• 
  
  
  

  
  

  Animation GIF représentant Fibonacci

  
  
  La plupart des êtres vivants sexués sont issus de deux parents, de sorte que leurs ancêtres à la n^e génération, supposés distincts, sont au nombre de 2ⁿ. Mais les hyménoptères sont tels que les femelles sont issues de deux parents, et les mâles sont issus d'une mère seulement. Il en résulte que leurs ancêtres à la n-ième génération sont constitués :pour les femelles, de Fn{displaystyle {mathcal {F}}_{n}} mâles et Fn+1{displaystyle {mathcal {F}}_{n+1}} femelles,pour les mâles, de Fn−1{displaystyle {mathcal {F}}_{n-1}} mâles et Fn{displaystyle {mathcal {F}}_{n}} femelles. Cette forme de reproduction asexuée décrit exactement la reproduction des abeilles. Récemment, une analyse mathématique et historique du contexte de Fibonacci et sa proximité de la ville de Béjaïa, une grande source de cire à l'époque (la version française du nom de cette ville est Bougie), a suggéré que c'était en fait les apiculteurs de Béjaïa et la connaissance de la reproduction des abeilles qui ont vraiment inspiré les nombres de Fibonacci plutôt que la reproduction des lapins^[17].

Généralisations |

Il existe plusieurs voies pour généraliser la suite de Fibonacci : on peut modifier les valeurs initiales, modifier les coefficients de la relation de récurrence ou modifier le nombre de termes (ou ordre) de la relation de récurrence.

Suites de Fibonacci généralisées |

On appelle suite de Fibonacci généralisée toute suite définie par la même relation de récurrence que la suite de Fibonacci, mais dont les termes initiaux sont différents de 0 et 1. Sur le modèle de la démonstration donnée plus haut (voir section Expression fonctionnelle), une telle suite un{displaystyle u_{n}} est encore de la forme αφn+βφ′n{displaystyle alpha varphi ^{n}+beta varphi '^{n}} où φ{displaystyle varphi } est le nombre d'or et φ′=−1/φ.{displaystyle varphi '=-1/varphi .} Elle est donc équivalente à αφn{displaystyle alpha varphi ^{n}}, sauf si α=0{displaystyle alpha =0} (ce qui ne se produit que si u1=φ′u0{displaystyle u_{1}=varphi 'u_{0}}), si bien que (comme la suite des quotients de la suite de Fibonacci) la suite un+1un{displaystyle {frac {u_{n+1}}{u_{n}}}} converge vers φ{displaystyle varphi }.

Parmi ces suites de nombres, il faut signaler les nombres de Lucas obtenus en choisissant comme initialisation : L0=2{displaystyle {mathcal {L}}_{0}=2} et L1=1{displaystyle {mathcal {L}}_{1}=1}. Cela donne la suite 2, 1, 3, 4, 7, 11, 18, 29,… On trouve parfois une initialisation L0=1{displaystyle {mathcal {L}}_{0}=1} et L1=3{displaystyle {mathcal {L}}_{1}=3} qui ne consiste qu'à décaler la suite d'un rang. Ces nombres interviennent dans la résolution d'équations diophantiennes. Ils sont très liés à la suite de Fibonacci, en particulier par la relation suivante : Ln=Fn+1+Fn−1{displaystyle {mathcal {L}}_{n}={mathcal {F}}_{n+1}+{mathcal {F}}_{n-1},} pour tout entier n > 0 (voir Propriétés, Propriété 9).

Suites de Lucas |

Ce sont les suites où la relation de récurrence a changé : elle est devenue

Xn+2=PXn−QXn+1.{displaystyle X_{n+2}=PX_{n}-QX_{n+1}.}

Elles sont de deux types, notés X = U et X = V, selon que l'initialisation est U0=0{displaystyle U_{0}=0} et U1=1{displaystyle U_{1}=1} ou qu'elle est V0=2{displaystyle V_{0}=2} et V1=P{displaystyle V_{1}=P}.

La suite de Fibonacci et la suite des nombres de Lucas sont les suites U et V de Lucas de paramètres P = 1 et Q = –1.

Suites de k-bonacci |

Ce sont des suites dont la relation de récurrence est d'ordre k. Un terme est la somme des k termes qui le précèdent

un+k=un+un+1+un+2+⋯+un+k−1{displaystyle u_{n+k},=,u_{n}+u_{n+1}+u_{n+2}+dots +u_{n+k-1}}

Parmi ces suites, on distingue la suite de Tribonacci (récurrence d'ordre 3) et la suite de Tetranacci (récurrence d'ordre 4). Selon ce nouveau classement de suites, la suite de Fibonacci est une suite de 2-bonacci.

Si on modifie tout à la fois (initialisation, récurrence, ordre) on arrive à l'ensemble très général des suites à récurrence linéaire.

Dans la culture |

Peinture |

Georges Seurat, Parade de cirque, 1887-1888

Dans son tableau Parade de cirque, peint en 1887-1888, Georges Seurat emploie les premiers termes de la suite : un personnage central, deux personnages à droite, trois musiciens, cinq banderoles ou cinq spectateurs en bas à gauche, huit à droite, treize en tout^[18].

Littérature |

• 
  Da Vinci Code, fiction de Dan Brown
  


• 
  LE SEMINAIRE livre XVI D'un Autre à l'autre, de Jacques Lacan, chapitre : Du pari de Pascal.

Cinéma |

Cette section ne cite pas suffisamment ses sources (avril 2013).  Pour l'améliorer, ajoutez des références vérifiables [comment faire ?] ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

Télévision |

Musique |

• Le groupe de metal progressif Tool structure le rythme de certaines parties du morceau Lateralus selon une suite de Fibonacci^[22].


• La chanteuse suisse pour enfants Sonia Grimm a publié sur son album Un petit lapin une chanson intitulée Le lapin de Fibonacci. Cette chanson présente aux enfants le nombre d'or et la suite de Fibonacci à travers l'exemple de la croissance d'une population de lapins^[23].


• Selon Ernő Lendvaï^[24], le compositeur Béla Bartók s'est régulièrement servi du nombre d'or et de la suite de Fibonacci dans ses œuvres. L'exemple le plus emblématique serait sa Musique pour cordes, percussion et célesta. Cependant, d'autres spécialistes de Bartók ont critiqué cette interprétation^[25].


• Le compositeur Iannis Xenakis a plusieurs fois utilisé la suite de Fibonacci : dès 1952 en tentant de créer une "image auditive" de cette série, puis dans quelques compositions : Zygia en 1952 et Le Sacrifice en 1953^[26].


• Sur la guitare de Robert Smith, chanteur de The Cure, pour la tournée 2016 du groupe, figure le début de la suite de Fibonacci^[27].

Architecture |

Le Corbusier et son Modulor, une mesure harmonique à l'échelle humaine applicable universellement à l'Architecture et à la mécanique.

• Illustrations architecturales


• 
  

  

  
  

  
  

  Cheminée d'usine à Unna.
  

  
  

  
  


• 
  

  

  
  

  
  

  Mole Antonelliana à Turin.
  

  
  

  
  

Mario Merz, Suite de Fibonacci, commande publique artistique, 1994, Strasbourg.

Jeux vidéo |

Dans le jeu Metal Gear Solid 4: Guns of the Patriots, la suite de Fibonacci apparaît en tant que petite comptine chantée par la petite Sunny.

Dans le jeu Watch Dogs, la suite de Fibonacci est introduite dans l'algorithme de Bellwether, capable de transmettre un message subliminal à travers le système ctOS.

Dans le jeu Elite sur BBC Micro, les développeurs ont utilisé la suite de Fibonacci pour permettre au jeu de tenir dans 22 ko. Le jeu génère donc aléatoirement la galaxie, mais il peut ensuite la générer exactement de la même façon lorsqu'une partie est sauvegardée puis rechargée.

Notes et références |

Voir aussi |

Bibliographie |

• 
  (en) Hrant Arakelian, Mathematics and History of the Golden Section, Logos 2014, 404 p. (ISBN 978-5-98704-663-0) (rus.)


• (en) J. H. Halton, « On the divisibility properties of Fibonacci numbers », Fibonacci Quarterly, vol. 4, n^o 3,‎ 1966, p. 217-240 (lire en ligne)


• 
  Nikolai Vorobiev (en), Caractères de divisibilité — Suite de Fibonacci, coll. Initiation aux Mathématiques, Éditions Mir, Moscou, 1973

Articles connexes |

• Groupe de Fibonacci


• Suite de Padovan


• Mot de Fibonacci


• Codage de Fibonacci


• The Fibonacci Association

Liens externes |

• Divisibilité des nombres de Fibonacci


• Suite de Fibonacci et nombre d'or dans l'ensemble de Mandelbrot


• Suite de Fibonacci dans le dictionnaire des nombres


• J.-C. Michel, « Le nombre d'or », sur gecif.net


• 
  « Les suites de Fibonacci aléatoires », 13 mai 2008, conférence de Benoît Rittaud à la Cité des sciences et de l'industrie
  


• (en) R. N. Knott et the Plus Team, « The life and numbers of Fibonacci », sur plus.maths.org, 4 novembre 2013

• Portail de l’analyse
• Portail des mathématiques