Krdytkyu

Pour les articles homonymes, voir Florence (homonymie).

Cet article est une ébauche concernant une localité de Caroline du Sud.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Florence.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")}

Géographie

Pays	États-Unis
État	Caroline du Sud
Comté	comté de Florence
Capitale de	Comté de Florence
Superficie	56,29 km2
Altitude	42 m
Coordonnées	34° 11′ 02″ N, 79° 46′ 27″ O

Démographie

Population	37 056 hab. (2010)
Densité	658,3 hab./km2 (2010)

Fonctionnement

Statut	Cité

Histoire

Fondation	24 décembre 1890

Identifiants

Code postal	29501–29506
Code FIPS	45-25810
GNIS	1222461
Indicatif téléphonique	843
Site web	(en) www.cityofflorence.com

modifier - modifier le code - modifier Wikidata

La ville de Florence (en anglais [ˈflɔrəns]) est le siège du comté de Florence, situé en Caroline du Sud, aux États-Unis.

Description |

Florence est l'une des principales villes de Caroline du Sud et la ville principale dans la région métropolitaine de Florence assise sur les deux comté de Florence et Darlington.

La population de la ville est en forte augmentation. Elle était 37 056 au recensement de 2010 et passe à 38 228 en estimation 2015. L'aire métropolitaine de Florence atteint 200 000 habitants.

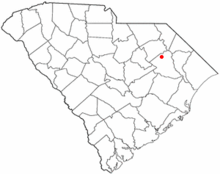
Florence se trouve à 110 km à l'est-nord-est de Columbia, la capitale de l'État. Elle conserve son statut de plaque tournante, à la fois pour l'industrie et les infrastructures, tout en s'établissant comme un centre régional pour les affaires, la médecine, la culture et la finance.

Démographie |

Source |

• 
  (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Florence, South Carolina » (voir la liste des auteurs).

Liens externes |

• Ressources relatives à la géographie : archINFORM • Geographic Names Information System • GeoNames


• (en) Site officiel

v · m Les 46 villes sièges de comtés de l’État de Caroline du Sud

.mw-parser-output .sep-liste{font-weight:bold} Abbeville · Aiken · Allendale · Anderson · Bamberg · Barnwell · Beaufort · Bennettsville · Bishopville · Camden · Charleston · Chester · Chesterfield · Columbia · Conway · Darlington · Dillon · Edgefield · Florence · Gaffney · Georgetown · Greenville · Greenwood · Hampton · Kingstree · Lancaster · Laurens · Lexington · Manning · Marion · McCormick · Moncks Corner · Newberry · Orangeburg · Pickens · Ridgeland · Saint George · Saint Matthews · Saluda · Spartanburg · Sumter · Union · Walhalla · Walterboro · Winnsboro · York

v · m Caroline du Sud
Régions	Plaine côtière atlantique · Montagnes Blue Ridge · Grand Strand · High Hills of Santee (en) · Lake Murray Country (en) · Lowcountry (en) · Metrolina · Midlands (en) · Ninety-Six District (en) · Olde English District (en) · Pee Dee (en) · Piedmont · Sandhills · Sea Islands · Upstate (en)
Principales villes	Charleston · Columbia · Greenville · Mount Pleasant · North Charleston · Rock Hill · Spartanburg
Villes moyennes	Aiken · Anderson · Beaufort · Bennettsville · Camden · Cayce · Conway · Easley · Florence · Forest Acres · Gaffney · Georgetown · Greenwood · Greer · Goose Creek · Hilton Head Island · Isle of Palms · Laurens · Lexington · Mauldin · Myrtle Beach · North Augusta (en) · North Myrtle Beach (en) · Orangeburg · Simpsonville (en) · Summerville · Sumter · Union · Walterboro · West Columbia (en) · York
Petites villes	Abbeville · Barnwell · Batesburg-Leesville (en) · Bluffton (en) · Clemson · Darlington · Dillon · Edgefield · Fort Mill · Fountain Inn (en) · Great Falls (en) · Hardeeville · Irmo · Jefferson (en) · Kingstree · Liberty (en) · Marion · McCormick · Moncks Corner · Newberry · Pageland (en) · Pendleton · Pickens · Seneca · Sullivan's Island · Travelers Rest (en) · Walhalla · Westminster · Williamston (en)
CDPs	Berea (en) · Carolina Forest (en) · Dentsville (en) · Gantt (en) · Ladson (en) · Parker (en) · Red Hill (en) · Saint Andrews (en) · Seven Oaks (en) · Socastee (en) · Taylors (en) · Wade Hampton (en)
Comtés	Abbeville · Aiken · Allendale · Anderson · Bamberg · Barnwell · Beaufort · Berkeley · Calhoun · Charleston · Cherokee · Chester · Chesterfield · Clarendon · Colleton · Darlington · Dillon · Dorchester · Edgefield · Fairfield · Florence · Georgetown · Greenville · Greenwood · Hampton · Horry · Jasper · Kershaw · Lancaster · Laurens · Lee · Lexington · Marion · Marlboro · McCormick · Newberry · Oconee · Orangeburg · Pickens · Richland · Saluda · Spartanburg · Sumter · Union · Williamsburg · York
Articles liés	Aéroports (en) · Census areas (en) · Collèges et universities (en) · Congressional districts (en) · Famous people · Gouverneurs · Highways (en) · Historic places (en) · History · Legislature · Radio stations (en) · Rivers (en) · Capitole · Parcs d'État · Television stations (en)
Société	Crime (en) · Culture · Démographie (en) · Économie · Éducation · Politique (en)

• Portail de la Caroline du Sud