Mačva (district)
Cette page contient des caractères cyrilliques. En cas de problème, consultez Aide:Unicode ou testez votre navigateur.
Pour les articles homonymes, voir Mačva.
Cet article est une ébauche concernant la Serbie et la géographie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
| Mačva.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")} | |
| Administration | |
|---|---|
Pays |  Serbie |
Villes ou municipalités | Bogatić Šabac Loznica Vladimirci Koceljeva Mali Zvornik Krupanj Ljubovija |
| Démographie | |
Population | 297 778 hab. (2011) |
| Densité | 91 hab./km2 |
| Géographie | |
Coordonnées | 44° 45′ 21″ nord, 19° 41′ 38″ est |
Superficie | 326 800 ha = 3 268 km2 |
| Localisation | |
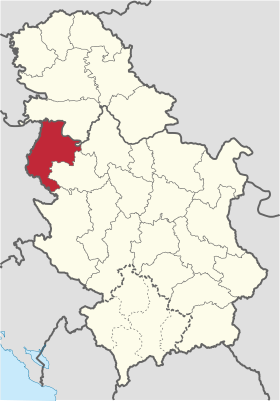 Localisation du district de Mačva en Serbie | |
Le district de Mačva (en serbe : Mačvanski okrug ; en serbe cyrillique : Мачвански округ) est une subdivision administrative de la République de Serbie. Au recensement de 2011, il comptait 297 778 habitants[1]. Le centre administratif du district de Mačva est la ville de Šabac.
Le district est situé à l’ouest de la Serbie, dans la région géographique de Mačva
Sommaire
1 Municipalités du district de Mačva
2 Autre
3 Références
4 Voir aussi
4.1 Articles connexes
Municipalités du district de Mačva |
| Nom | Superficie (en km²) | Population 2002[2] | Population 2011[1] | Statut |
|---|---|---|---|---|
| Bogatić | 384 | 32 990 | 28 879 | Municipalité |
| Vladimirci | 338 | 20 373 | 17 291 | Municipalité |
| Koceljeva | 257 | 15 636 | 13 155 | Municipalité |
| Krupanj | 342 | 20 192 | 17 398 | Municipalité |
| Loznica | 612 | 86 413 | 78 788 | Ville |
| Ljubovija | 356 | 17 052 | 14 424 | Municipalité |
| Mali Zvornik | 184 | 14 076 | 12 496 | Municipalité |
| Šabac | 795 | 122 893 | 115 347 | Ville |
| Total | 3 268 | 329 625 | 297 778 |
Autre |
La région de Šabac comporte des monuments célèbres ; certains sont dédiés aux événements de l’histoire du peuple serbe, comme le Monument en l’honneur de Karageorges et des Héros serbes de la première révolte contre les Turcs ou le Musée de la bataille de Mišar ; mais on y trouve aussi le palais du roi Stefan Milutin et la forteresse médiévale du mont Cer.
Non loin de Loznica se trouve le village de Tršić, qui vit naître Vuk Stefanović Karadžić, le grand réformateur de la langue serbe. Le monastère de Tronoša remonte à la dynastie des Nemanjić ; ce monastère, grâce à ses moines copistes, a joué un rôle important dans la préservation de la culture serbe.
Références |
(sr + en) « Livre 20 : Vue d'ensemble comparative de la population en 1948, 1953, 1961, 1971, 1981, 1991, 2002 et 2011, données par localités) » [PDF], Pages du recensement de 2011 en Serbie - Institut de statistique de la République de Serbie, 2014(consulté le 23 septembre 2015)
(sr) Population, analyse comparative de la population en 1948, 1953, 1961, 1971, 1981, 1991 et 2002, données par localités (Livre 9), Belgrade, Institut de statistique de la République de Serbie, mai 2004(ISBN 86-84433-14-9)
Voir aussi |
.mw-parser-output .autres-projets ul{margin:0;padding:0}.mw-parser-output .autres-projets li{list-style-type:none;list-style-image:none;margin:0.2em 0;text-indent:0;padding-left:24px;min-height:20px;text-align:left}.mw-parser-output .autres-projets .titre{text-align:center;margin:0.2em 0}.mw-parser-output .autres-projets li a{font-style:italic}
Articles connexes |
- Districts de Serbie
- Municipalités de Serbie
- Villes de Serbie
Subdivisions de la Serbie
Portail de la Serbie et du peuple serbe
