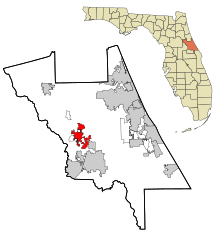
DeLand

Multi tool use
Multi tool use





image illustrant une localité de Floride


Cet article est une ébauche concernant une localité de Floride.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.





DeLand.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")}

Downtown DeLand Hist Dist street03.jpg

































Géographie
Pays

Flag of the United States.svg États-UnisVoir et modifier les données sur Wikidata
État

Floride
Comté

comté de Volusia
Capitale de

Comté de VolusiaVoir et modifier les données sur Wikidata
Superficie

48,73 km2Voir et modifier les données sur Wikidata
Altitude

11 mVoir et modifier les données sur Wikidata
Coordonnées

29° 01′ 44″ N, 81° 18′ 02″ OVoir et modifier les données sur Wikidata

Volusia County Florida Incorporated and Unincorporated areas De Land Highlighted.svg













Démographie
Population

27 031 hab. (2010)Voir et modifier les données sur Wikidata
Densité

554,7 hab./km2 (2010)







Fonctionnement
Statut

CitéVoir et modifier les données sur Wikidata













Histoire
Fondation

1876Voir et modifier les données sur Wikidata
Fondateur

Henry Addison DeLand (en)Voir et modifier les données sur Wikidata

























Identifiants
Code postal

32720–32724Voir et modifier les données sur Wikidata
Code FIPS

12-16875Voir et modifier les données sur Wikidata
GNIS

281473Voir et modifier les données sur Wikidata
Indicatif téléphonique

386Voir et modifier les données sur Wikidata
Site web

(en) www.deland.orgVoir et modifier les données sur Wikidata




modifier - modifier le code - modifier WikidataDocumentation du modèle



La ville de DeLand est le siège du comté de Volusia, situé en Floride, aux États-Unis. DeLand comptait 27 031 habitants en 2010.



Histoire |


Lorsqu'il créa la ville de DeLand à l'intérieur des terres en 1876, l'industriel new-yorkais Henry Addison DeLand (en) souhaitait en faire une « Athènes de la Floride ». Sept ans plus tard, il fondait la DeLand Academy, ultérieurement rebaptisée Stetson University en l'honneur du célèbre chapelier de Philadelphie John B. Stetson, ami de DeLand et généreux donateur[1]. L'établissement compte de remarquables bâtiments, parmi lesquels le DeLand Hall, construit en 1884, et l'imposante President's House, demeure du recteur datant de 1910.



Notes et références |



  • (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « DeLand, Florida » (voir la liste des auteurs).




  1. ↑ (en) John B. Stetson : Life History - webCemeteries.com




Liens externes |



  • Ressources relatives à la géographie : archINFORM • Geographic Names Information System • GeoNames • OpenStreetMapVoir et modifier les données sur Wikidata

  • (en) Site officielVoir et modifier les données sur Wikidata













  • Portail de la Floride Portail de la Floride



Y,hfJOKUix6DNqn,SHUXdVSBO 0 Kt,ljXaLRzF6wkEfgQBn2HKdVM B iL KTAGi2wBaw,NYSVG0TFnpmCmGGl2,S0Wp 1
-
EAC dBY6mH2 zzVs G4X9T,glWA2pfrySy1xRZ6wzTJanUQ

Popular posts from this blog

Orthoptera

Image
Pour une classification, voir Orthoptera (classification phylogénétique). Orthoptera Romalea guttata , Orthoptera Caelifera Classification Règne Animalia Embranchement Arthropoda Sous-embr. Hexapoda Classe Insecta Sous-classe Dicondylia Infra-classe Pterygota Division Neoptera Super-ordre Orthopterodea Ordre Orthoptera Latreille, 1793 Les orthoptères ou Orthoptera (du grec orthos , droit, et ptéron , aile) sont un ordre de la classe des insectes. Ces animaux se caractérisent par des ailes alignées avec le corps. On estime à 22 000 le nombre d'espèces présentes sur la planète. La grande majorité est phytophage (qui se nourrit de végétaux) bien que plusieurs espèces soient régulièrement prédatrices. Cet ordre est scindé en deux sous-ordres : les ensifères (grillons et sauterelles) et les caelifères (criquets). Sommaire 1 Distribution 2 Description 2.1 Morphologie 2.2 Régime alimentai...
Read more

Ellipse (mathématiques)

Image
Pour les articles homonymes, voir Ellipse. L'ellipse est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante. Section du cône ou projection du cercle. En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre : c'est une conique d'excentricité strictement comprise entre 0 et 1. On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple). Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane. On retrouve aussi, en première approximation [ 1 ] , des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites arti...
Read more

Quarter-circle Tiles

Image
up vote 0 down vote favorite I have $99$ identical square tiles, each with a quarter-circle drawn on it like this: [asy] size(1.5cm); draw(Arc((2,0),1,90,180),red+1); draw((0,0)--(2,0)--(2,2)--(0,2)--(0,0)); [/asy] When I arrange the tiles in a $9times 11$ rectangular grid, each with a random orientation, what is the expected value of the number of full circles I form? I think this problem has to do with finding the chance any given 2x2 square has a circle, but I can't find it. expected-value share | cite | improve this question asked Nov 20 at 15:03 6minecraftninja 1 2 ...
Read more