Loi de Weibull
































































Weibull

Image illustrative de l’article Loi de Weibull
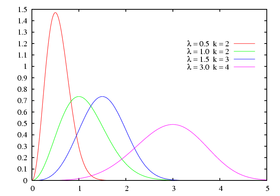Densité de probabilité


Image illustrative de l’article Loi de Weibull
Fonction de répartition
Paramètres
λ>0{displaystyle lambda >0,}lambda >0, échelle (réel)
k>0{displaystyle k>0,}k>0, forme (réel)

Support
x∈[0;+∞[{displaystyle xin [0;+infty [,}xin [0;+infty [,

Densité de probabilité
(k/λ)(x/λ)(k−1)e−(x/λ)k{displaystyle (k/lambda )(x/lambda )^{(k-1)}e^{-(x/lambda )^{k}}}(k/lambda )(x/lambda )^{{(k-1)}}e^{{-(x/lambda )^{k}}}

Fonction de répartition
1−e−(x/λ)k{displaystyle 1-e^{-(x/lambda )^{k}}}1-e^{{-(x/lambda )^{k}}}

Espérance
μ=λΓ(1+1k){displaystyle mu =lambda Gamma left(1+{frac {1}{k}}right),}mu =lambda Gamma left(1+{frac {1}{k}}right),

Médiane
λ(ln⁡2)1/k{displaystyle lambda (ln 2)^{1/k},}{displaystyle lambda (ln 2)^{1/k},}

Mode
λ(k−1k)1k{displaystyle lambda left({frac {k-1}{k}}right)^{frac {1}{k}},}{displaystyle lambda left({frac {k-1}{k}}right)^{frac {1}{k}},} si k>1{displaystyle k>1}k>1

Variance
σ2=λ2Γ(1+2k)−μ2{displaystyle sigma ^{2}=lambda ^{2}Gamma left(1+{frac {2}{k}}right)-mu ^{2},}sigma ^{2}=lambda ^{2}Gamma left(1+{frac {2}{k}}right)-mu ^{2},

Asymétrie
γ1=λ3Γ(1+3k)−3μσ2−μ3σ3{displaystyle gamma _{1}={frac {lambda ^{3}Gamma (1+{frac {3}{k}})-3mu sigma ^{2}-mu ^{3}}{sigma ^{3}}}}gamma _{1}={frac {lambda ^{3}Gamma (1+{frac {3}{k}})-3mu sigma ^{2}-mu ^{3}}{sigma ^{3}}}

Kurtosis normalisé
γ2=λ4Γ(1+4k)−4μσ3γ1−3σ4−6μ2σ2−μ4σ4{displaystyle gamma _{2}={tfrac {lambda ^{4}Gamma (1+{frac {4}{k}})-4mu sigma ^{3}gamma _{1}-3sigma ^{4}-6mu ^{2}sigma ^{2}-mu ^{4}}{sigma ^{4}}}}{displaystyle gamma _{2}={tfrac {lambda ^{4}Gamma (1+{frac {4}{k}})-4mu sigma ^{3}gamma _{1}-3sigma ^{4}-6mu ^{2}sigma ^{2}-mu ^{4}}{sigma ^{4}}}}

Entropie
γ(1−1k)+(λk)k+ln⁡(λk){displaystyle gamma left(1!-!{frac {1}{k}}right)+left({frac {lambda }{k}}right)^{k}+ln left({frac {lambda }{k}}right)}{displaystyle gamma left(1!-!{frac {1}{k}}right)+left({frac {lambda }{k}}right)^{k}+ln left({frac {lambda }{k}}right)}

Fonction génératrice des moments
mn=λnΓ(1+n/k){displaystyle m_{n}=lambda ^{n}Gamma (1+n/k),}m_{n}=lambda ^{n}Gamma (1+n/k),

modifier Consultez la documentation du modèle

En théorie des probabilités, la loi de Weibull, nommée d'après Waloddi Weibull en 1951, est une loi de probabilité continue.
La loi de Weibull est un cas spécial de loi d'extremum généralisée au même titre que la loi de Gumbel ou la loi de Fréchet.




Sommaire






  • 1 Fonctions caractéristiques


  • 2 Utilisation pratique


    • 2.1 Liens avec d'autres lois


    • 2.2 Généralités


    • 2.3 Analyse de défaillances


      • 2.3.1 Détermination des paramètres de la loi


      • 2.3.2 Exploitation des données




    • 2.4 Application pour les aéro-générateurs (éoliennes)


    • 2.5 Application en science des matériaux




  • 3 Bibliographie


  • 4 Notes et références


  • 5 Voir aussi


    • 5.1 Articles connexes


    • 5.2 Liens externes







Fonctions caractéristiques |


Avec deux paramètres (pour x>0) la densité de probabilité est :


f(x;k,λ)=kλ(xλ)k−1e−(x/λ)k{displaystyle f(x;k,lambda )={frac {k}{lambda }}left({frac {x}{lambda }}right)^{k-1}operatorname {e} ^{-(x/lambda )^{k}},}f(x;k,lambda )={frac {k}{lambda }}left({frac {x}{lambda }}right)^{{k-1}}operatorname {e}^{{-(x/lambda )^{k}}},

où




  • k > 0 est le paramètre de forme et

  • λ > 0 le paramètre d'échelle de la distribution.


Sa fonction de survie est définie par


S(x;k,λ)=e−(x/λ)k,{displaystyle mathrm {S} (x;k,lambda )=operatorname {e} ^{-(x/lambda )^{k}},}{displaystyle mathrm {S} (x;k,lambda )=operatorname {e} ^{-(x/lambda )^{k}},}

et sa fonction de répartition complémentaire de défaillance est définie par


F(x;k,λ)=1−e−(x/λ)k.{displaystyle F(x;k,lambda )=1-operatorname {e} ^{-(x/lambda )^{k}}.}{displaystyle F(x;k,lambda )=1-operatorname {e} ^{-(x/lambda )^{k}}.}

Avec trois paramètres (loi généralisée, domaine x>θ) , sa densité de probabilité est :



f(x;k,λ,θ)=kλ(x−θλ)k−1e−(x−θλ)k{displaystyle f(x;k,lambda ,theta )={frac {k}{lambda }}left({frac {x-theta }{lambda }}right)^{k-1}operatorname {e} ^{-left({frac {x-theta }{lambda }}right)^{k}},}{displaystyle f(x;k,lambda ,theta )={frac {k}{lambda }}left({frac {x-theta }{lambda }}right)^{k-1}operatorname {e} ^{-left({frac {x-theta }{lambda }}right)^{k}},} pour x ≥ θ et ƒ(x ; k, λ, θ) = 0 pour x < θ,

où k > 0 est le paramètre de forme, λ > 0 est le paramètre d'échelle et θ est le paramètre de position de la distribution.


Sa fonction de répartition est définie par :


F(x;k,λ,θ)=1−e−(x−θλ)k{displaystyle F(x;k,lambda ,theta )=1-operatorname {e} ^{-left({frac {x-theta }{lambda }}right)^{k}}}{displaystyle F(x;k,lambda ,theta )=1-operatorname {e} ^{-left({frac {x-theta }{lambda }}right)^{k}}}

pour x ≥ θ, et


F(x ; k, λ, θ) = 0 pour x < θ.

Le coefficient d'asymétrie est donné par :


γ1=λ3Γ(1+3k)−3μσ2−μ3σ3{displaystyle gamma _{1}={frac {lambda ^{3}Gamma (1+{frac {3}{k}})-3mu sigma ^{2}-mu ^{3}}{sigma ^{3}}}}gamma _{1}={frac {lambda ^{3}Gamma (1+{frac {3}{k}})-3mu sigma ^{2}-mu ^{3}}{sigma ^{3}}}

Le kurtosis non normalisé est donné par :


β2=λ4Γ(1+4k)−4μσ3γ1−6μ2σ2−μ4σ4{displaystyle beta _{2}={frac {lambda ^{4}Gamma (1+{frac {4}{k}})-4mu sigma ^{3}gamma _{1}-6mu ^{2}sigma ^{2}-mu ^{4}}{sigma ^{4}}}}beta _{2}={frac {lambda ^{4}Gamma (1+{frac {4}{k}})-4mu sigma ^{3}gamma _{1}-6mu ^{2}sigma ^{2}-mu ^{4}}{sigma ^{4}}}

Le taux de panne h est donné par :


h(x;k,λ,θ)=kλ(x−θλ)k−1.{displaystyle h(x;k,lambda ,theta )={frac {k}{lambda }}left({frac {x-theta }{lambda }}right)^{k-1}.}h(x;k,lambda ,theta )={frac {k}{lambda }}left({frac {x-theta }{lambda }}right)^{{k-1}}.

La loi d'extremum généralisée de type III est un retournement de la loi de Weibull. Son domaine est x ≤ θ . Sa fonction de répartition est définie par :


F(x;k,λ,θ)=e−(θ−xλ)k.{displaystyle F(x;k,lambda ,theta )=operatorname {e} ^{-left({frac {theta -x}{lambda }}right)^{k}}.}{displaystyle F(x;k,lambda ,theta )=operatorname {e} ^{-left({frac {theta -x}{lambda }}right)^{k}}.}


Utilisation pratique |



Liens avec d'autres lois |


Si X∼Weibull(k=α,λ=m){displaystyle mathrm {X} sim {textrm {Weibull}}(k=alpha ,lambda =m)}{mathrm {X}}sim {textrm {Weibull}}(k=alpha ,lambda =m) , alors m2X∼Frechet(α,s,m){displaystyle {tfrac {m^{2}}{mathrm {X} }}sim {textrm {Frechet}}(alpha ,s,m)}{tfrac {m^{2}}{{mathrm {X}}}}sim {textrm {Frechet}}(alpha ,s,m).


Si X∼Weibull{displaystyle mathrm {X} sim {textrm {Weibull}}}{displaystyle mathrm {X} sim {textrm {Weibull}}} , alors log⁡(X)∼Gumbel{displaystyle log(X)sim {textrm {Gumbel}}}log(X)sim {textrm {Gumbel}}.


Si Xk∼Exp(λ){displaystyle mathrm {X} ^{k}sim {textrm {Exp}}(lambda )}{mathrm {X}}^{k}sim {textrm {Exp}}(lambda ), alors X∼Weibull(k,λ){displaystyle mathrm {X} sim {textrm {Weibull}}(k,lambda )}{mathrm {X}}sim {textrm {Weibull}}(k,lambda )



Généralités |


L'expression loi de Weibull recouvre en fait toute une famille de lois, certaines d'entre elles apparaissant en physique comme conséquence de certaines hypothèses. C'est, en particulier, le cas de la loi exponentielle (k = 1) et de la loi de Rayleigh (k = 2) importantes en matière de processus stochastique.


Ces lois constituent surtout des approximations particulièrement utiles dans des techniques diverses alors qu'il serait très difficile et sans grand intérêt de justifier une forme particulière de loi. De ce point de vue elles sont analogues à la loi normale qui remplace efficacement des distributions (presque) symétriques. Une distribution à valeurs positives (ou, plus généralement mais moins fréquemment, à valeurs supérieures à une valeur donnée) a presque toujours la même allure. Elle part d'une fréquence d'apparition nulle, croît jusqu'à un maximum et décroît plus lentement. Il est alors possible de trouver dans la famille de Weibull une loi qui ne s'éloigne pas trop des données disponibles en calculant k et λ à partir de la moyenne et la variance observées.



Analyse de défaillances |



Détermination des paramètres de la loi |




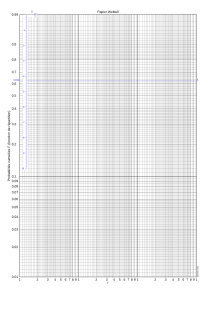
Papier Weibull vierge.


La distribution de Weibull est souvent utilisée dans le domaine de l'analyse de la durée de vie, grâce à sa flexibilité : comme dit précédemment, elle permet de représenter au moins approximativement une infinité de lois de probabilité.


Articles détaillés : Loi de fiabilité et Analyse de survie.

Le paramètre x est ici le temps, noté t. Dans ce domaine, on note souvent



  • α le paramètre d'échelle (noté ici λ) ;

  • β le paramètre de forme (noté ici k) ;

  • γ le paramètre de position (noté ici θ) ;

  • on définit parfois le paramètre d'échelle « vrai » η = α1/β = λ1/k ; parfois, on utilise η pour noter le paramètre d'échelle « classique » (η = α = λ).


On définit la fiabilité


R(t)=1−F(t)=e−(t−θλ)k=e−(t−θ)kη{displaystyle R(t)=1-F(t)=operatorname {e} ^{-left({frac {t-theta }{lambda }}right)^{k}}=operatorname {e} ^{-{frac {(t-theta )^{k}}{eta }}}}{displaystyle R(t)=1-F(t)=operatorname {e} ^{-left({frac {t-theta }{lambda }}right)^{k}}=operatorname {e} ^{-{frac {(t-theta )^{k}}{eta }}}}

On voit que l'on peut linéariser la loi en utilisant des logarithmes :



ln⁡(−ln⁡R(t))=k(ln⁡(t−θ)−ln⁡λ)=kln⁡(t−θ)−ln⁡η{displaystyle ln(-ln R(t))=k(ln(t-theta )-ln lambda )=kln(t-theta )-ln eta }{displaystyle ln(-ln R(t))=k(ln(t-theta )-ln lambda )=kln(t-theta )-ln eta } ;

si le facteur de position est nul (θ = 0), on a alors


ln⁡(−ln⁡R(t))=k(ln⁡t−ln⁡λ)=kln⁡t−kln⁡λ{displaystyle ln(-ln R(t))=k(ln t-ln lambda )=kln t-kln lambda }{displaystyle ln(-ln R(t))=k(ln t-ln lambda )=kln t-kln lambda }

on voit donc que moyennant un changement de variable


x=ln⁡t,y=ln⁡(−ln⁡(1−F));{displaystyle x=ln t,,,y=ln(-ln(1-F));}{displaystyle x=ln t,,,y=ln(-ln(1-F));}

on a une loi affine


y=k(x−ln⁡(λ)){displaystyle y=k(x-ln(lambda ))}{displaystyle y=k(x-ln(lambda ))}

On peut donc déterminer graphiquement les paramètres de la loi de Weibull :



  1. On collecte les données : durée de vie t d'un appareil.

  2. On détermine les probabilités cumulées F(t).

  3. On place les points F(t) sur un diagramme « loglog/log », appelé « papier Weibull » ou « papier Allen Plait ».

  4. Si l'on peut faire passer une droite par régression, alors θ = 0 ; on peut déterminer λ à partir de l'ordonnée à l'origine, et k à partir de la pente.


Pour être plus précis : lorsque t = λ, on a


F=1−e−1≈0,632,R(λ)=e−1⟹ln⁡(−ln⁡R(λ))=ln⁡(1)=0.{displaystyle F=1-mathrm {e} ^{-1}approx 0,632,,R(lambda )=mathrm {e} ^{-1}quad Longrightarrow ln(-ln R(lambda ))=ln(1)=0.}{displaystyle F=1-mathrm {e} ^{-1}approx 0,632,,R(lambda )=mathrm {e} ^{-1}quad Longrightarrow ln(-ln R(lambda ))=ln(1)=0.}

Le paramètre d'échelle λ est donc l'abscisse t à laquelle la droite de régression coupe la droite horizontale F = 0,632 (axe y = 0 du diagramme loglog/log).


Concernant l'échelle de la pente, on peut prendre deux points remarquables pour une pente de k = 1. Par exemple, en choisissant arbitrairement λ = 1, la droite passe par les points (1 ; 0,9) et (2 ; 0,99). On peut ainsi construire une échelle des pentes.


Le cas où θ est non nul est un peu plus délicat. Les outils informatiques permettent d'ajuster la loi à trois paramètres (c'est un cas de régression non linéaire), mais il faut se poser la pertinence de ce modèle :



  • si θ > 0, cela signifie que l'on a un intervalle de temps sans aucune défaillance ; graphiquement, la courbe sur un papier Weibull est convexe (arrondi vers le bas) ;

  • si θ < 0, cela signifie que l'on a des défaillances avant mise en service ; graphiquement, la courbe sur un papier Weibull est concave (arrondi vers le haut).


Il faut avoir au moins une vingtaine de points pour pouvoir estimer que la courbe n'est pas linéaire, voire plus si θ est proche de zéro.


Si l'on veut faire une détermination purement graphique des paramètres, il faut « décaler l'axe des temps » — qui est, rappelons-le, logarithmique — jusqu'à obtenir une droite.



Exploitation des données |




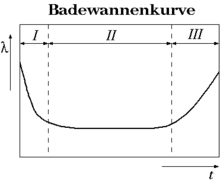
Courbe en baignoire


La compréhension du taux de panne peut fournir une indication au sujet de la cause des pannes, et donc de mettre en place des actions correctives. Les fabricants et distributeurs ont tout intérêt à bien maitriser ces informations par type de produits afin d'adapter :



  • les durées de garantie (gratuites ou payantes) ;

  • la planification de la maintenance (entretien, voir MTBF).


Il faut distinguer la défaillance d'un système complet et la défaillance d'un composant[1]. Pour un composant, le paramètre de forme k peut indiquer la nature de la défaillance, et l'analyse du taux de panne est une aide précieuse dans la maîtrise des procédés de fabrication et de mise en œuvre. Le paramètre d'échelle λ va indiquer quand la panne a le plus de probabilité de se produire.


Pour un système complet, le paramètre de forme k n'a pas de sens physique. Seul le paramètre λ peut nous donner une information pour la maintenance.


Si le taux de panne diminue au cours du temps alors, k < 1. Un taux de panne décroissant relève d'une « mortalité infantile » (« défaillances de jeunesse »). Ainsi, les éléments défectueux tombent en panne rapidement, et le taux de panne diminue au cours du temps, quand les éléments fragiles sortent de la population.


Si le taux de panne est constant dans le temps alors, k = 1. Un taux de panne constant suggère que les pannes sont liées à une cause stationnaire.


Si le taux de panne augmente avec le temps alors, k > 1. Un taux de panne croissant suggère une « usure ou un problème de fiabilité » : les éléments ont de plus en plus de chances de tomber en panne quand le temps passe.


Dans un certain nombre de cas, et notamment en électronique, la courbe de taux de panne est en « forme de baignoire » — selon le système, baignoire sabot ou piscine. Cela indique que l'on a dans un premier temps des défaillances rapides dues à des défauts de fabrication. Puis, on a une période stable, et enfin une usure.


Si l'on veut éviter des pannes de jeunesse en service, on peut mettre les composants en fonctionnement sur des bancs, afin de repérer les composants défaillants et de ne livrer que des composants exempts de défauts de jeunesse. Le passage au banc éventuellement dans des conditions de vieillissement accéléré pour réduire la durée avant mise en service. Il faut toutefois faire attention à ne pas provoquer non plus d'usure prématurée, donc de se placer au début de la partie plate de la courbe.


Dans le cas de systèmes mécaniques, c'est l'usure et la corrosion qui prédominent, on a en général une courbe toujours croissante (k > 1).



Application pour les aéro-générateurs (éoliennes) |


La distribution de Weibull est utilisée pour estimer le potentiel éolien d'un site.
Elle modélise la probabilité qu'un vent souffle à telle vitesse sur ce site.



Application en science des matériaux |


Parmi les différents modèles permettant de décrire la variation statistique de la contrainte à la rupture d'un matériau, la distribution de Weibull est la plus couramment utilisée[2]. Le paramètre de forme k est appelé couramment le module de Weibull et permet de donner une idée de la dispersion sur la taille des défauts dans le matériau. Plus il est faible, et plus cette dispersion est importante (e.g.: k proche de 10, pour une céramique industrielle avec une répartition homogène de défauts de même taille). Enfin, la constante λ représente la contrainte de rupture moyenne de l’échantillon de volume.



Bibliographie |



  • Waloddi Weibull, A statistical distribution function of wide applicability, J. Appl. Mech.-Trans. ASME, 18(3), 1951 [présentation en ligne]


Notes et références |





  1. ↑ (Reliability tools: Weibull analysis, Barringer & Associates, Inc.


  2. ↑ Anderson T. L., Fracture Mechanics – Fundamentals and Applications, 3rd Edition, Taylor & Francis Ed., 2005.




Voir aussi |



Articles connexes |



  • Loi d'extremum généralisée

  • Loi de Rayleigh

  • Loi de Fréchet

  • Loi de Gumbel



Liens externes |


  • Logiciel d'analyse de données de survie Weibull++, utilisant entre autres, la distribution de Weibull.


























v · m


Lois de probabilité (liste)







































































































































  • Portail des probabilités et de la statistique Portail des probabilités et de la statistique



-

Popular posts from this blog

Ellipse (mathématiques)

Image
Pour les articles homonymes, voir Ellipse. L'ellipse est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante. Section du cône ou projection du cercle. En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre : c'est une conique d'excentricité strictement comprise entre 0 et 1. On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple). Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane. On retrouve aussi, en première approximation [ 1 ] , des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites arti...
Read more

Quarter-circle Tiles

Image
up vote 0 down vote favorite I have $99$ identical square tiles, each with a quarter-circle drawn on it like this: [asy] size(1.5cm); draw(Arc((2,0),1,90,180),red+1); draw((0,0)--(2,0)--(2,2)--(0,2)--(0,0)); [/asy] When I arrange the tiles in a $9times 11$ rectangular grid, each with a random orientation, what is the expected value of the number of full circles I form? I think this problem has to do with finding the chance any given 2x2 square has a circle, but I can't find it. expected-value share | cite | improve this question asked Nov 20 at 15:03 6minecraftninja 1 2 ...
Read more

Mont Emei

Image
Mont Emei.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")} Vue du sommet Wanfo du mont Emei Géographie Altitude 3 099  m , Wanfo Coordonnées 29° 31′ 11″ nord, 103° 19′ 57″ est Administration Pays   Chine Province Sichuan Ville-préfecture Leshan Géolocalisation sur la carte : Sichuan Mont Emei Géolocalisation sur la carte : Chine Mont Emei modifier   Paysage panoramique du mont Emei, incluant le paysage panoramique du grand Bouddha de Leshan *   Patrimoine mondial de l'UNESCO Passerelle en bois sur le versant ouest Pays   Chine Subdivision Sichuan Type Mixte Critères (iv) (vi) (x) Superficie 15 400 ha Numéro d’identification 779 Zone géographique Asie et Pacifique  ** Année d’inscription 1996 (20 e session) * Descriptif officiel UNESCO ** Classification géog...
Read more